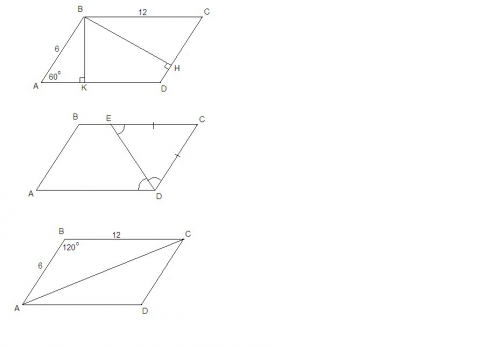
.В параллелограмме ABCD AD=12см, AB=6см, уголBAD=60градусов.
1
площадь S=AB*AD*sin60=12*5*√3/2 =30√3 см2
площадь S=AB*h1 ; h1 = S/AB = 30√3 / 6= 5√3 <---высота 1
площадь S=AD*h2 ; h2 = S/AD = 30√3 / 12= 2,5√3 <---высота 2
2
угол <BAD=60градусов
угоп <D = 180 - <BAD = 180 - 60 =120 град <D / 2 = 120 /2=60
<C =<BAD=60градусов
Биссектриса угла D пересекает BC в точке Е.
треугольник ECD -равносторонний , так как все углы 60 град
стороны треугольника ECD тоже равны b =DE=EC=CD=AB= 6 см
радиус описанной окружности R = b√3/3 =6*√3/3=2√3 см
длина окружности L=2R*п=2*2√3*п=4п√3 см <обычно в таком виде
3
длина большей диагонали параллелограмма. - по теореме косинусов
d^2 = AB^2+AD^2 - 2*AB*AD*cos <D
d^2 = 6^2 +12^2 -2*6*12 *cos120 =252
d = √252 = 6√7 <--длина большей диагонали
Объяснение:
1) ΔDBE - равнобедренный по условию, следовательно,
BD = BE и ∠BDE = ∠BED
2) Рассмотрим ΔАВЕ и ΔDBC
BE = BD и ∠BEА =∠BDС = (т.к. ΔDBE - равнобедренный)
∠ABE = ∠DBC по условию
ΔАВЕ = ΔDBC по стороне и 2-м прилежащим к ней углам, значит
АВ = ВС, т.е. ΔАВС - равнобедренный, ч.т.д.
б) ∠ BDA + ∠BDE = 180°, т.к. это смежные углы
∠ ВЕС + ∠BED = 180°
∠ BDA + ∠ВЕС + 2∠BDE = 360° (∠BDE = ∠BED, см. выше)
230° + 2∠BDE = 360°
∠BDE = 130°/2 = 65°