Дуга AB = 80°
Объяснение:
Дано:
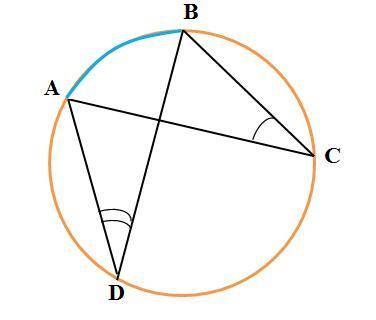
в окружности (см. рисунок)
∠ADB - вписанный угол
∠ACB - вписанный угол
∠ADB+∠ACB=80°
Найти: дуга AB
Решение.
Вписанные углы ∠ADB и ∠ACB опираются на дугу AB.
Далее применим следующие свойства вписанных углов:
Теорема 1. Вписанные углы, опирающиеся на одну и ту же дугу равны.
Теорема 2. Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу.
По теореме 1: ∠ADB=∠ACB. Тогда из ∠ADB+∠ACB=80° следует:
∠ADB+∠ADB=80° или 2·∠ADB=80°.
По теореме 2: дуга AB = 2·∠ADB. Отсюда дуга AB = 2·∠ADB = 80°.
Для начала вспомним, что тупой угол - это угол с градусной мерой больше 90° и меньше 180°. Из одной точки можно пустить три луча, которые между собой образуют 3 тупых угла.
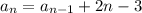 , где n - число лучей кратное 3.
, где n - число лучей кратное 3.
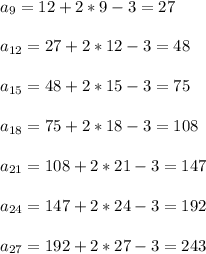
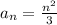
Пустим 4-й луч вблизи одного из трёх лучей, у нас добавится дополнительно 2 тупых угла. 5-й луч пустим вблизи второго из числа первых трёх, дополнительно образуются 3 тупых угла. Наконец, пускаем 6-й луч вблизи третьего, получив дополнительно 4 тупых угла. У нас будет получаться как бы три пучка близко расположенных лучей в каждом пучке.
Считаем сколько получилось тупых углов после добаления к первым трём лучам ещё трёх лучей. 3 луча было, плюс 2, плюс 3 и плюс 4, всего 12 лучей.
Итак, для 3-х лучей - 3 тупых угла; для 6 лучей - 12 тупых углов.
Рассуждаем аналогично, добавляя по очереди ещё 3 луча. Добавятся сначало 4 угла, затем 5 и, наконец, 6; т.е. всего добавится 15 тупых углов. А всего для 9 лучей будет 27 тупых углов.
Точно также, считая для 12 лучей, получим дополнительно 6+7+8 = 21 тупых угла, а всего - 48.
Можно было бы и далее продолжать таким но мы замечаем закономерность.
Пусть а1 = 3 - это первый член последовательности. Используя предыдущее значение (рекуррентно), можно вычислить следующее значение по формуле:
Пробуем вычислить по этой формуле:
Итак, ответ найден. Для 27 лучей возможно максимум 243 тупых угла.
Так считать долго, можно увидеть формулу для прямого расчёта:
По этой формуле можно считать для любого количества лучей, кратное трём.