Поскольку плоскость сечения параллельна оси цилиндра, сечением будет прямоугольник с высотой H, равной высоте цилиндра, и основанием длиной L, являющемся хордой, лежащей в основании цилиндра. Также известно, что диагональ прямоугольника имеет наклон в 60 градусов к его основанию. Отсюда можно записать следующие соотношения:
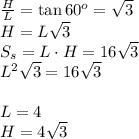
Далее проведем отрезки, соединяющие концы хорды с центром основания цилиндра. Получится равнобедренный треугольник с углом в вершине 120 градусов и бедрами, равными радиусу основания цилиндра. Проведя в этом треугольнике высоту из вешины к хорде, получим два прямоугольных треугольника, одним из катетов которых является половина хорды. Поскольку угол между этими катетами и гипотенузой равен 30 градусам, можно записать следующее соотношение между длиной хорды и радиусом основания цилиндра:
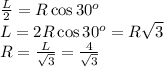
Запишем теперь выражение для площади боковой поверхности цилиндра:
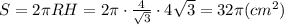
ответ: Площадь боковой поверхности цилиндра равна 32пи кв. см
Объяснение:
1) Третий признак подобия треугольников: пропорциональны три стороны.
Сопоставим стороны треугольников ABC и ACD:
Меньшая сторона: BC = 8, CD = 12
Средняя сторона: AB = 12, AC = 18
Большая сторона: AC = 18, AD = 27
Все эти три пары относятся друг к другу как 2 к 3
BC / CD = 8 / 12 = 2 / 3
AB / AC = 12 / 18 = 2 / 3
AC / AD = 18 / 27 = 2 / 3
Отсюда следует, что треугольники подобны, что и требовалось доказать.
2) Первый признак подобия треугольников:
Два угла равны
Рассмотрим треугольники KBP и ABC
Угол ABC - общий
Углы KPB и BAC равны по условию
Значит, у этих треугольников соблюдается равенство двух углов, значит, они подобны.
3) Второй признак подобия:
Две стороны треугольников пропорциональны и углы, заключающие эти стороны, равны.
AB * BK = CB * BP
Разделим выражение на CB
(AB / CB) * BK = BP
Разделим выражение на BK
AB / CB = BP / BK
Угол ABC - общий, он заключает пропорциональные стороны треугольников, значит, треугольник ABC подобен треугольнику KBP.