Рассмотрим равнобедренный треугольник ABC с боковыми сторонами AB = BC и основанием AC.
Опустим из вершины B высоту BH на основание AC.
Рассмотрим треугольники ABH и BCH.
Так как BH - высота, то углы BHA = BHC = 90°, т.е. треугольники ABH и BCH - прямоугольные.
Заметим, что AB = BC, т.е. гипотенузы треугольников ABH и BCH равны и у них общий катет BH.
Следовательно, треугольники ABH и BCH конгруэнтны по гипотенузе и катету.
Отсюда вытекает, что AH = CH, а это означает, что BH является медианой.
Также из равенства треугольников ABH и BCH имеем, что углы ABH = CBH.
Следовательно, BH является биссектрисой угла ABC.
1. У окружности с центром на прямой y=4 и касающейся оси абсцисс радиус, очевидно, будет равен 4. Общее уравнение окружности с центром (a;b):
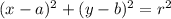
Из простейших геометрических соображений, центр будет лежать на пересечении прямых x=3 и y=4. Итак, центр: (3;4). Уравнение окружности будет иметь вид:
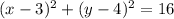
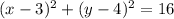и 
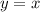. Решим подстановки. Подставим х в первое уравнение вместо y.
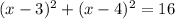. После раскрытия скобок получаем:
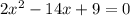. Решив его, получим ответы:
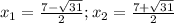. Так как точки лежат на прямой y=x, то эти точки будут записываться так: 
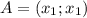и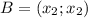 
, где вместо 
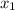и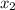 
подставляем числа, найденные выше.
2. Решим систему уравнений:
В целом вот так. Проверяйте на ошибки!