
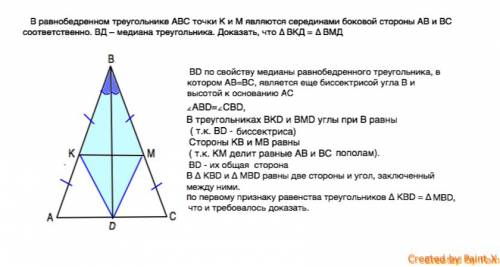
В равнобедренном треугольнике АВС точки К и М являются серединами боковой стороны АВ и ВС соответственно. ВД – медиана треугольника. Доказать, что ∆ ВКД = ∆ ВМД
ВД по свойству медианы равнобедренного треугольника, в котором АВ=ВС, является еще биссектрисой угла В и высотой к основанию АС
∠АВД=∠СВД,
В треугольниках ВКД и ВМД углы при В равны ( ВД - биссектриса угла АВС)
Стороны КВ и МВ равны ( т.к. КМ делит равные АВ и ВС пополам).
ВД - их общая сторона
В ∆ КВД и ∆ МВД равны две стороны и угол, заключенный между ними.
По первому признаку равенства треугольников ∆ КВД = ∆ МВД, что и требовалось доказать.
Номер 1
Можно даже не вычислять,чему равны углы 1;2;3;
Два угла 30 градусов называются соответственными,если при пересечении двух прямых секущей соответственные углы равны,то прямые параллельны
<1=<30=30 градусов,как накрест лежащие,вообще-то-смотрятс каким из двух углом сравнивать
<1+<2=180 градусов,как односторонние
<2=180-30=150 градусов
Если при пересечении двух прямых секущей односторонние углы в сумме равны 180 градусов,то прямые параллельны
<3=<2=150 градусов,как вертикальные
Номер 2
<20=<2=<20 градусов,как вертикальные
Если угол 3 в 8 раз больше угла 2,то
<3=20•8=160 градусов
<3=20+160=180 градусов
Если при пересечении двух прямых секущей односторонние углы в сумме равны 180 градусов,то прямые параллельны
<4=<3=160 градусов,как накрест лежащие
<5=<2=20 градусов
Объяснение: