3. Сумма углов ΔАВЕ=180°. Значит ∠АЕВ=180-∠ВАЕ-∠АВЕ=180-40-75=65°
∠АЕВ=∠ADCтрапеции т.к. ВЕ║CD. ∠ADC=65° Сумма углов трапеции, прилежащих к боковой стороне равна 180°. Значит ∠АВС=180-40=140° и ∠BCD=180-65=115°
8. Сумма углов трапеции, прилежащих к боковой стороне равна 180°. Значит ∠АВС=180-50=130°
∠ABD=90° дано по условию (см. чертеж). ΔBCD равнобедренный, т.к. ВС=CD (по чертежу). ∠CBD равнобедренного ΔBCD равен 130-90=40°
Углы при основании равнобедренного треугольника равны, значит ∠CDB=∠CBD=40°. Сумма углов треугольника равна 180°, поэтому ∠BCD=180-40-40=100°
∠CDA трапеции равен 180-100=80°, т.к. сумма углов при боковой стороне трапеции равна 180°
Объяснение:
8см
Объяснение:
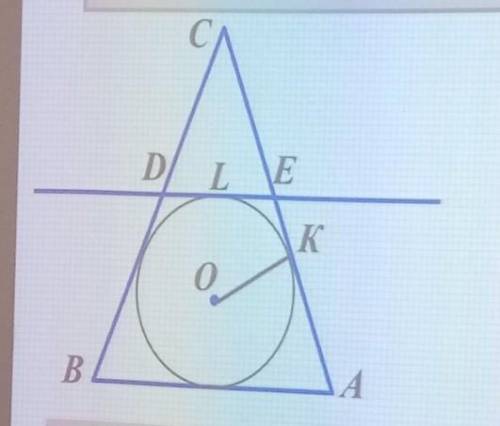
Теорема: Отрезки касательных к окружности, проведенные из одной точки, равны:
1) BM = BF MD = DL
FA = KA EK = LE
2) Pcde = CD + DE + CE =
= CD + (DL + LE) + CE = (CD + MD) + (EK +CE) = CM + CK =
= (BC - BM) + (AC - AK)
Т.к. ΔАВС - равнобедренный, то
ВС = АС = (Pabc - AB)/2 = (20 - 6)/2 = 7(cм)
Pcde = ВС + АС - ВМ - АК = 2 * 7 - ВМ - АК = 14 - ВМ - АК
3) Центр вписанной окружности лежит на биссектрисе. Но в равнобедренном треугольнике высота, а так же медиана и биссектриса, проведенные к основанию совпадают, следовательно, СF - медиана и делит АВ пополам:
ВF = FA = 6 / 2 = 3 (см)
4) Т.к. отрезки касательных к окружности, проведенные из одной точки, равны, то
BF = BM = 3(см)
FA = AK = 3(см)
Pcde = 14- ВМ - АК = 14 -2*3 = 8(см)