Пусть S₁ - это площадь бо́льшего треугольника, а S₂ - площадь меньшего треугольника.
Пусть k > 1 (это значит, что в числителе будет стоять бо́льший треугольник).
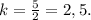
Отсюда -
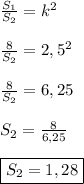
1,28 (ед²).
- - -
Случай 2 - Площадь меньшего треугольника равна 8 (ед²).В этом случае наоборот k < 1 (в числителе будет стоять меньший треугольник).
S₁ - площадь бо́льшего треугольника, S₂ - площадь меньшего треугольника
Тогда -
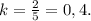
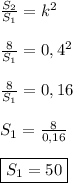
50 (ед²).
Теорема. Центр окружности, вписанной в треугольник, является точкой пересечения его биссектрис.
Доказательство. Пусть ABC – данный треугольник, O – центр вписанной в него окружности, D, E и F – точки касания окружности со сторонами. Прямоугольные треугольники AOD и AOE равны по гипотенузе и катету. У них гипотенуза AO общая, а катеты OD и OE равны как радиусы. Из равенства треугольников следует равенство углов OAD и OAE. А это значит, что точка O лежит на биссектрисе треугольника, проведённой из вершины A. Точно так же доказывается, что точка O лежит на двух других биссектрисах треугольника. Теорема доказана.
Объяснение: