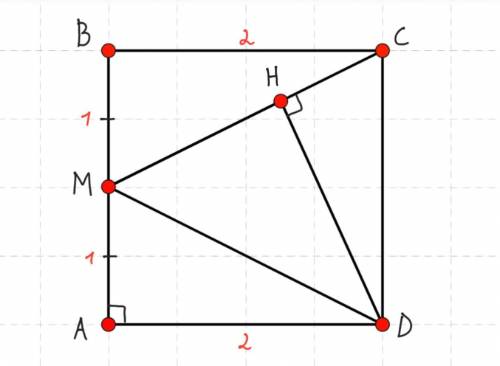
Дано: ABCD — квадрат, Sabcd= 4, т.М — середина АВ, АМ=ВМ, DH⟂СМ.
Найти: DH.
Решение.
1) Найдем сторону квадрата.
АВ²= 4;
АВ= 2 (–2 не подходит).
AB=BC=CD=AD= 2.
т.M — середина АВ, значит, АМ=ВМ= 2:2= 1.
2) Мы видим два равных прямоугольных треугольника: ΔMBC и ΔMAD (равны по двум катетам).
Найдем их площадь. Площадь прямоугольного треугольника равна половине произведения его катетов.
Значит, Smbc= Smad= ½•1•2= 1.
3) А площадь треугольника MDC равна разности площади квадрата и площадей треугольников MBC и MAD.
Т.е. Smdc= Sabcd–Smbc–Smad= 4–1–1= 4–2= 2.
4) Найдем сторону МС прямоугольного треугольника МВС (МС - это гипотенуза) по т.Пифагора:
МС²= МВ²+ВС²;
МС²= 1+2²;
МС²= 5;
МС= √5
5) Площадь обычного (произвольного) треугольника равна произведению половины основания этого треугольника на высоту, проведённую к этому основанию.
Для треугольника MDC это выглядит так:
Smdc= ½•MC•DH.
2= ½•√5•DH;
2 : ½ = √5DH;
√5DH= 4;
DH= 4/√5.
Расстояние от вершины D квадрата ABCD до прямой СМ равно 4/√5.
ОТВЕТ: 4/√5.
Приклад 1. З вершини квадрата АВСD проведено перпендикуляр АК до площини квадрата. Знайти площу квадрата, якщо КD = 5 см; КС = 13 см.Розв’язання (мал. 416). 1) АК АВС; КD - похила; АDБ - її проекція. Оскільки АD DС, то за теоремою про три перпендикуляри маємо КD DС.3) Тоді площа квадрата S = 82 = 64 (см2).
Приклад 2. Сторони трикутника довжиною 4 см, 13 см і 15 см. Через вершину найбільшого кута до площини трикутника проведено перпендикуляр і з його кінця, що не належить трикутнику, проведено перпендикуляр завдовжки 4 см до протилежної сторони цього кута. Знайти довжину перпендикуляра, проведеного до площини трикутника.Розв’язання. 1) У ∆АВС: АВ = 4 см; ВС = 13 см; АС = 15 см. Оскільки АС - найбільша сторона трикутника, то АВС - найбільший кут трикутника. ВК АВС (мал. 417).2) КМ АС, тоді за теоремою про три перпендикуляри: ВМ АС, тобто ВМ - висота ∆АВС. За умовою: КМ = 4см.3) Знайдемо площу трикутника АВС за формулою Герона.4) 3 іншого боку