0
Объяснение:
Противоположные стороны равны, отсюда следует что в данный четырехугольник можно вписать окружность, а центр окружности совпадает с точкой пересечения биссектрис(но это не точно)), далее, расстояние-это перпендикуляр, поэтому проводим перпендикуляр к DR и к OR,так как окружность касается к этим сторонам, то перпедикуляры MC и ME- радиусы вписанной окружности, которые между собой равны, и значит их разность = 0. Но это не точное решение, лучше перепроверить,тут просто 1 предположение,которое я не могу доказать.
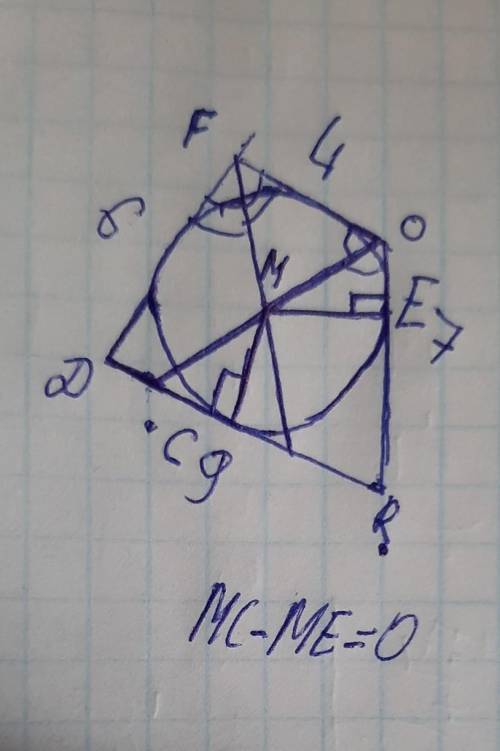
А) Сумма острых углов в прямоугольном треугольнике = 90°.
Пусть один угол из них = х, тогда второй острый угол = 90° - х
б) сумма внешних углов = 180°
Для угла = х внешний угол = 180° -х
для другого угла внешний угол = 180° -(90° -х) = 180° - 90° +х= 90° +х
в) (180° - х)/(90° +х) =12/15
(180° - х)/(90° +х) =4/5
5(180° - х) = 4(90° +х)
900 - 5х = 360 + 4х
9х = 540
х = 60° ( это один острый угол данного прямоугольного треугольника)
90° - 60° = 30°( это второй острый угол)
ответ: 60° и 30°