
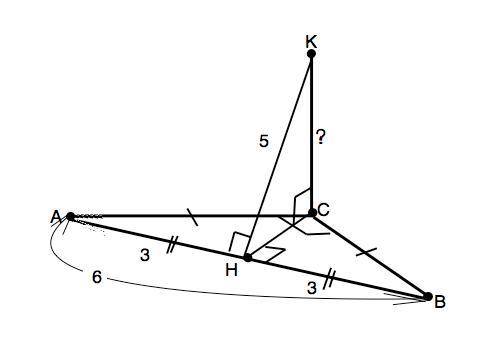
Треугольник АВС - равнобедренный прямоугольный с прямым углом С и гипотенузой 6 см. Отрезок СК перпендикулярен к плоскости треугольника. Расстояние от К до прямой АВ равно 5 см. Найдите длину отрезка СК.
ответ: 4 см
Объяснение:
Расстояние до АМ от К измеряется длиной проведенного перпендикулярно к ней отрезка КН. КН⊥АВ ⇒ по т. о трех перпендикулярах СН⊥АВ, а т.к. треугольник АВС - равнобедренный прямоугольный. то СН его высота и медиана, и по свойству медианы прямоугольного треугольника равна СН=АВ:2=6:2=3.
По свойству прямой, перпендикулярной плоскости, отрезок СК перпендикулярен всем прямым, лежащим в ней. ⇒ КС⊥СН Из прямоугольного ∆ КСН по т.Пифагора КС=√(KH²-CH²)=√(25-9)=4 (см).
АВ²=8²+15²=64+225=289
АВ=√289=17(см)
Точка А по условию задачи равноудалена от вершин Δ, значит АВ=АД=АС=17см