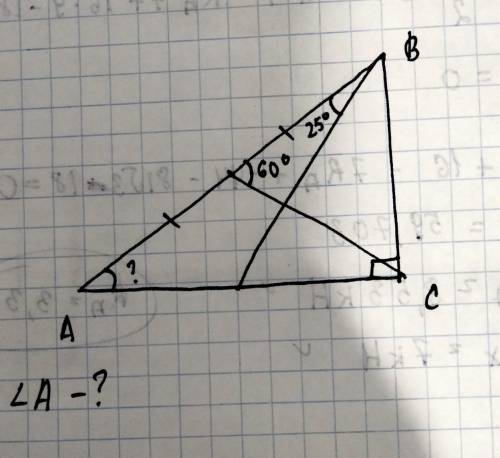
Объяснение:
Если провести медиану ВN к стороне АС, то по ее свойству (медиана делит сторону пополам) АN = NC
Выбираем произвольное место на медиане и поставим там точку М, если от точек А и С провести прямые к М, то мы получим треугольник АМС, в котором есть медиана МN. По условию сказано, что АМ = МС, а значит, что треугольник равнобедренный с основанием АС, как и треугольник АВС. По скольку эти два треугольника имеют общую основу - АС и их медианы накладываются друг на друга, лёжа с середины АС и пересекая противолежащий угол, значит и треугольник АВС тоже равнобедренный => АВ = ВС
В Δ ABC - прямоугольном, проведена медиана CM из вершины прямого угла => AM=MB=CM (по свойству медианы в прямоугольном треугольнике)
Р/м ΔAMC
AM=CM => ΔAMC - р/б => ∠A=∠MCA
∠BMO и ∠AMH - смежные, их сумма 180 градусов => ∠AMH=180-60=120°
Сумма углов треугольника равна 180 градусов, углы при основании равны => ∠A=∠MCA=(180-120)/2=60/2=30°
ответ: 30°
Объяснение: