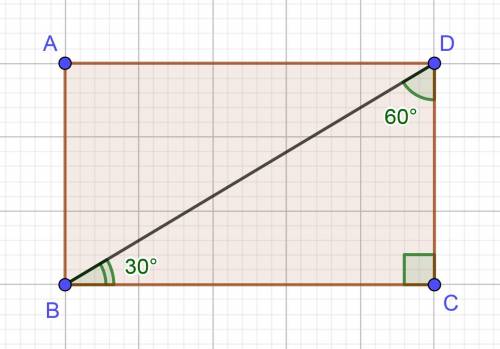
Нехай дано прямокутник ABCD, BD — діагональ, DC = 10 см, ∠BDC = 60°.
Р-мо BDC:
∠BCD = 90° — як кут прямокутника, отже ΔBDC — прямий, ∠BDC = 60° — за умовою, тоді ∠DBC за теоремою про суму кутів трикутника буде дорівнювати:
∠DBC = 180°−90°−60° = 30°.
По властивості катета, який лежить напроти кута 30°, гіпотенуза трикутника буде рівна:
BD = 2*DC = 2*10 = 20 (cm)
Знайдемо інший катет за т. Піфагора:
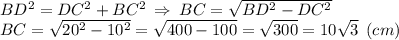
Підставимо значення у формулу площі прямокутника:

Відповідь: Площа прямокутника рівна 100√3 см² або приблизно 173,2 см².
Знайдемо радіус основи:
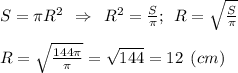
Діаметр d (AB) = 2R = 2*12 = 24 (см)
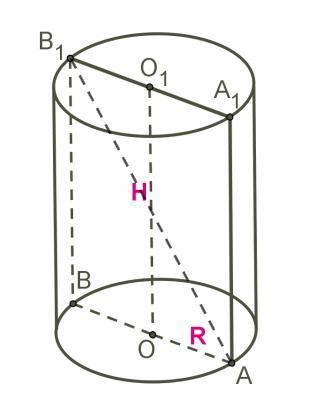
Осовий переріз — це прямокутник (AA₁B₁B), перпендикулярний основі, який проходить через центральну вісь циліндра. AB₁ - діагональ, яка ділить осьовий переріз на два конгруентні прямокутні трикутники, і являється гіпотенузою.
Розглянемо ΔAB₁B:
∠B = 90° ⇒ ΔAB₁B — прямокутний. AB₁ = 25 см, АВ = 24 см. Знайдемо невідомого довжину катета B₁B.
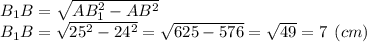
Будь-яка твірна циліндра є його висотою: BB = h = 7 (см)
Розглянемо прямокутник AA₁B₁B:
AA₁B₁B — це осьовий переріз, який являє собою прямокутник з шириною AB = 24 см та висотою B₁B = 7 см. Знайдемо площу:
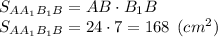
Відповідь: довжина твірної циліндра рівна 7 см, площа осьового перерізу циліндра рівна 168 см².
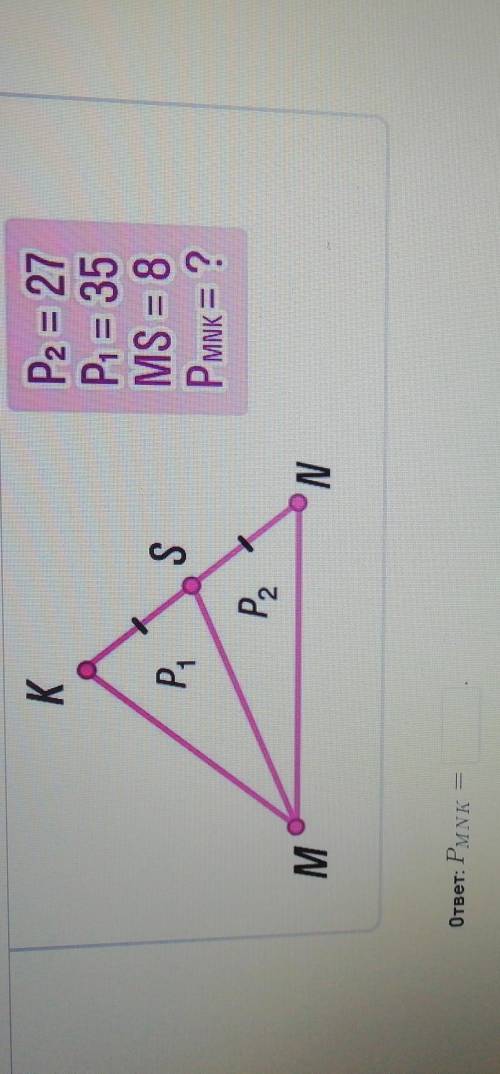
Если сложить периметры заданных треугольников, то получим периметр треугольника MNK плюс два отрезка MS.
ответ: P(MNK) = 27 + 35 - 2*8 = 62 - 16 = 46.