Так как отрезки РР₁ и ММ₁ перпендикулярны плоскости а, то указанные отрезки лежат на одной плоскости, а точка Р₁ лежит на отрезке КМ₁.
Рассмотрим ∆КРР₁ и ∆КММ₁.
Угол МКМ₁ – общий;
Угол КР₁Р=угол КМ₁М (оба прямые, так как РР₁ и ММ₁ перпендикулярны КМ₁)
Следовательно ∆КРР₁~∆КММ₁ по двум углам.
Пусть КР=n, тогда РМ=2n (из отношения КР:РМ=1:2), следовательно КМ=KP+PM=n+2n=3n.
Отношение двух любых сторон одного треугольника, равно отношению двух соответствующих сторон треугольника, подобного первому. Тогда:
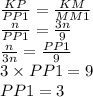
ответ: 3 см
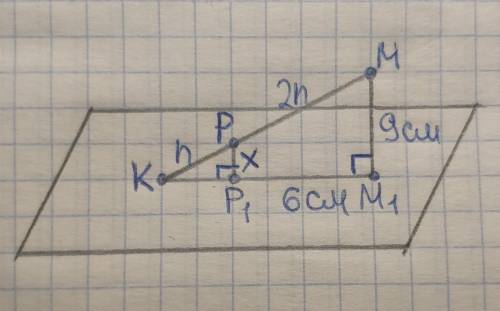
1) Якщо трикутника ABC і FDK , то їх відповідні елементи теж рівні:
AB = FD, BC = DK, CA = KF
∠A = ∠F, ∠B = ∠D, ∠C = ∠K
Відповідно, якщо відрізок AC = 6 см, то відповідний йому відрізок — KF — теж рівний 6 см.
Якщо кут С = 60°, то відповідний йому кут — K — теж рівний 60°.
2) ∠AOB = ∠DOC — так як вертикальні
ВО = ОС, AO = OD — за умовою
Маємо трикутники АОВ та DOC, у яких рівні дві сторони та кут між ними. А це перша ознака рівності трикутників.
Отже, ΔАОВ = ΔDOC
У рівних трикутників рівні і відповідні елементи:
AO = DO, BO = CO, AB = DC
Отже, AB = DC як відповідні еленти у ріних трикутниках.
3) Позначимо одну із сторін трикутника за х (см), тоді другу за х−6 (см), а третю – за х+10 (см). Периметр трикутника рівний 70. Складемо і розв'яжемо рівняння:
x+x−6+x+10 = 70
3x+4 = 70
3x = 66
x = 22
x = 22 см — довжина однієї сторони трикутника
х−6 = 22−6 = 16 см — довжина другої сторони трикутника
х+10 = 22+10 = 32 см — довжина третьої сторони трикутника
Відповідь: Довжини сторін трикутника рівні 16, 22 та 32 см.
Объяснение:
ответ на эту задачу в картине