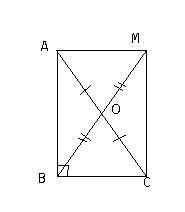
Рассмотрим прямоугольный треугольник ABC (угол B - прямой, BO - медиана). Угол B опирается на дугу AB, а так как угол B - вписанный, то дуга AB равна 2*уголB = 180. Следовательно AC - диаметр, а центр AC - центр окружности. Но окружность так же проходит по точке B. А значит AO = OC = OB = r - радиус описанной окружности.
Доказано Надо доказать, что BO = AO = OC
Рассмотрим прямоугольный треугольник ABC (угол B - прямой, BO - медиана). Продолжим BO, на линии отложим отрезок равный BO: OM (рисунок прилагается). Соединим точку M с точками A и C. Получится четырехугольник ABCM. Рассмотрим треугольники AOM и COB:
<AOM = <BOC (вертикальные углы)
AO = OC (О - середина AC)
BO = OM (по построению)
По 1 признаку равенства треугольников, ΔMOA = ΔBOC, следовательно все элементы в этих треугольниках равны:
АМ = BC; <MAC = <ACB - накрест лежащие углы. Так как накрест лежащие углы равны, то AM параллельно BC. По признаку параллелограмма (две противолежащие стороны равны и параллельны) четырехугольник ABCM является Параллелограммом. Но угол B - прямой, а значит параллелограмм является прямоугольником, а в прямоугольнике диагонали равны.
AC = BM - значит и их половины равны:
BO = AO = OC = OM
Что и требовалось доказать
В равнобедренном треугольнике биссектрисы, проведённые к боковым сторонам, равны.
Доказательство: Пусть ABC - равнобедренный треугольник (AC = BC), AK и BL - его биссектрисы. Треугольники AKB и ALB равны по второму признаку равенства треугольников. У них сторона AB общая, углы LAB и KBA равны как углы при основании равнобедренного треугольника, а углы LBA и KAB равны как половины углов при основании равнобедренного треугольника. Так как треугольники равны, их стороны AK и LB - биссектрисы треугольника ABC - равны. Теорема доказана.