
Дано :
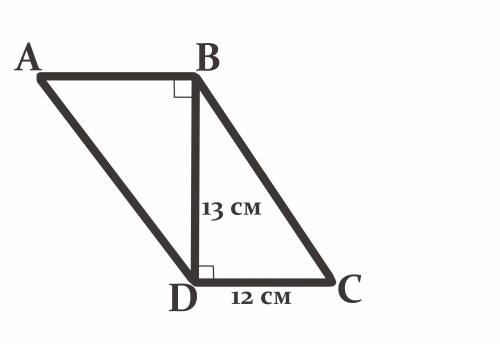
Четырёхугольник ABCD - параллелограмм.
Отрезок DB - диагональ = 13 см.
∠ABD = 90°.
CD = 12 см.
Найти :
S(ABCD) = ?
AB ║ CD (по определению параллелограмма).
Рассмотрим накрест лежащие ∠ABD и ∠BDC при параллельных прямых АВ и CD и секущей BD.
При пересечении двух прямых секущей накрест лежащие углы равны.То есть -
∠ABD = ∠BDC = 90°.
Тогда отрезок BD - ещё и высота параллелограмма ABCD (по определению).
Площадь параллелограмма равна произведению его стороны и высоты, опущенной на эту сторону.Следовательно -
S(ABCD) = BD*CD
S(ABCD) = 13 см*12 см
S(ABCD) = 156 см².
156 см².
Объяснение:
6)
<МКN=180°, развернутый угол
<МКР=<МКN-<PKN=180°-40°=140°
<PKS=<SKN, по условию
<РKS=<PKN/2=40°/2=20°
<MKS=<MKP+<PKS=140°+20°=160°
ответ: <MKS=160°
9)
<KLN=180°, развернутый угол.
<RLN=<KLN-KLR=180°-40°=140°
<KLT=<TLR, по условию.
<ТLR=<KLR/2=40°/2=20°
<TLN=<TLR+<RLN=20°+140°=160°
ответ: <TLN=160°
7)
<ACB=180°, развернутый угол.
<АCD=<ACB-<BCD=180°-120°=60°
<ACE=<ECD, по условию.
<ЕСD=<ACD/2=60°/2=30°
<BCE=<ECD+<BCD=30°+120°=150°
ответ: <ВСЕ=150°
1- BC= BK+KC= 15=9= 24(см)
2- АК- биссектриса, то укол 1=углу 2
3-BC||AD, AK-СЕКУЩАЯ, то угол 3= углу 2 как накрест лежащие, но угол 1=углу 2, тогда 1=3, значит треугольник АВК- равнобедренный, то АВ=ВК= 15 см
4- 2(АВ+ВС)= 2(15+24*)= 2*39= 78 см
ответ: 78 см
*24- это bk=ck