Стороны треугольника имеют длины : 8 дм , 10дм , 13,5 дм. Найти длины отрезков, на которые биссектриса большего угла делит противоположную сторону .
БОльший угол расположен против бОльшей стороны . Пусть бОльшая сторона АС=13,5 дм, тогда против неё лежит бОльший угол В .
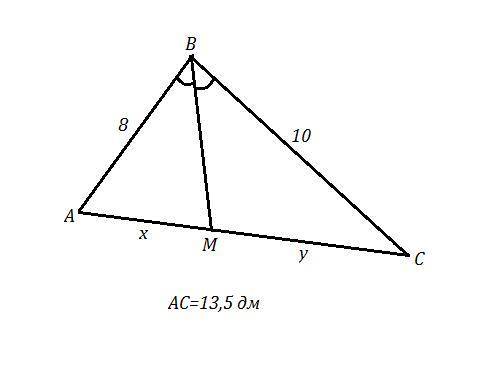
ΔАВС , АВ=8 дм , ВС=10 дм , АС=13,5 дм . ВМ - биссектриса.
Обозначим АМ=х , СМ=у .
По свойству биссектрисы угла треугольника: 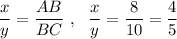 .
.
Тогда x=4k , y=5k ⇒ AC=AM+CM=x+y=4k+5k=9k , 9k=13,5 , k=1,5
AM=4k=4·1,5=6 дм
BC=5k=5·1,5=7,5 дм
1. Каждая сторона треугольника меньше суммы двух других сторон. Пользуясь этой теоремой, пишем неравенства для сторон шестиугольника.
2. Неравенство для второго вопроса -
PK+KL+LM+MN+NR+PR < PA+KA+DK+DL+LB+BM+ME+EN+NC+RC+PF+FR.
3. Неравенство для третьего вопроса -
2*(PK+KL+LM+MN+NR+PR) < PA+KA+DK+DL+LB+BM+ME+EN+NC+RC+PF+FR+(PK+KL+LM+MN+NR+PR).
4. На картинке.
5. Пользуемся ответами от 3 и 4 задания.Сумма периметров треугольников АВС и DEF равна 16 см (7 см+9 см). Я не знаю, там нужно писать единицы измерения или нет.
Вот такое неравенство в итоге получилось -
2*(PK+KL+LM+MN+NR+PR) < 16 см.
6. Логично, что поделить на 2.
Получаем, что -
2*(PK+KL+LM+MN+NR+PR) < 16 см
PK+KL+LM+MN+NR+PR < 8 см.
В прямоугольной трапеции ABCD (AD ║ BC) ∠A = 90°, BC = CD = 5 см, AD = 8 см. Найдите площадь трапеции.
Опустим из точки С на основание AD перпендикуляр CH ⇒
Получим прямоугольник ABCН (AD ║ BC, BA ║ CH, ∠A = 90°)
Значит, BA = CH, BC = AH = 5 см, HD = AD - AH = 8 - 5 = 3 см
В прямоугольном треугольнике CHD: По теореме Пифагора
CD² = CH² + HD² ⇒ CH² = CD² - HD²
CH² = 5² - 3² = 25 - 9 = 16 ⇒ CH = ВА = 4 см
Площадь прямоугольной трапеции ABCD равна:
S = (BC + AD) * CH/2 = (5 + 8) * 4/2 = 13 * 2 = 26 см²
ответ: 26 см².
Объяснение:
возможно неправильною