Грани правильного тетраэдра - равносторонние треугольники.
Их биссектриса является и высотой и медианой.
В сечении образуется равнобедренный треугольник, одна сторона которого равна ребру тетраэдра, две других - высоты грани.
Высота грани h = a*cos 30° = a√3/2 = 5√3/2.
Площадь сечения можно определить или 1) по формуле Герона, или 2) через высоту сечения.
1) Полупериметр p = 6,83013. Площадь S = √(p(p-a)(p-b)(p-c).
Поставив данные, получаем:
S = √( 6,83013*1,830123*2,5*2,5) = √78,125 = 8,83883.
2) Высота сечения из середины ребра на противоположное ребро равна:
h(c) = √(h² - (a/2)²) = √(18,75 - 6,25) = √12,5 ≈ 4,33013.
S = (1/2)*h(c)*a = (1/2)*5*4,330135 = 8,83883.
Построение на рисунке в приложении.
Объяснение:
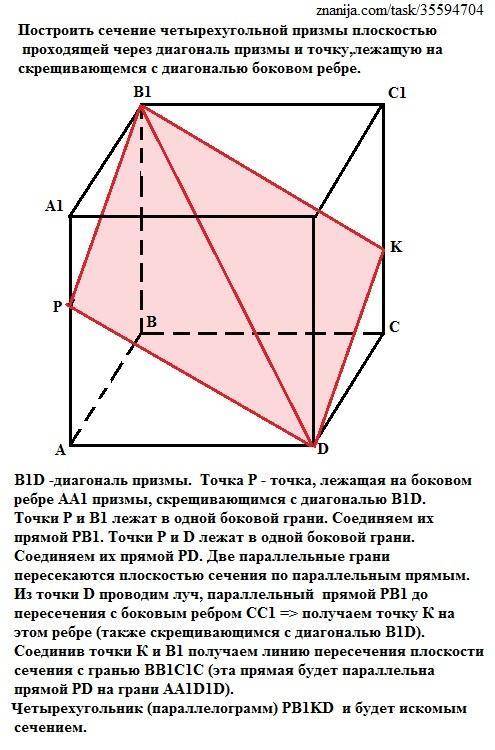
B1D -диагональ призмы. Точка Р - точка, лежащая на боковом ребре АА1 призмы, скрещивающимся с диагональю В1D.
Точки Р и В1 лежат в одной боковой грани. Соединяем их прямой РВ1. Точки Р и D лежат в одной боковой грани. Соединяем их прямой РD. Две параллельные грани пересекаются плоскостью сечения по параллельным прямым. Из точки D проводим луч, параллельный прямой РВ1 до пересечения с боковым ребром СС1 => получаем точку К на этом ребре (также скрещивающимся с диагональю B1D).
Соединив точки К и В1 получаем линию пересечения плоскости сечения с гранью ВВ1С1С (эта прямая будет параллельна прямой PD на грани AA1D1D). Четырехугольник (параллелограмм) PB1KD и будет искомым сечением.
Угол ABD = 118°; Угол DBC = 62°;
Объяснение:
Угол ABD это x, значит угол DBC x-56, значит:
1) x+x-56=180
2x-56=180
2x=180+56
2x=236
x=118
Угол ABD равен 118°
2) 118-56=62
Угол DBC = 62°