
Сколько плоскостей можно провести через 2 точки?
ответ: бесчисленное множество.
Объяснение: Из аксиом планиметрии: Через любые две точки можно провести прямую и притом только одну.
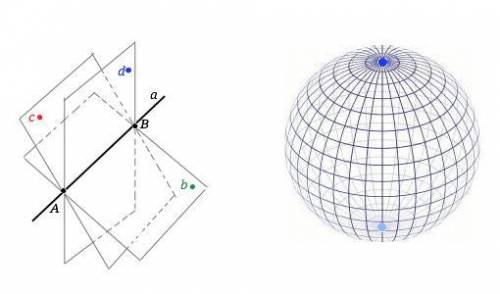
Через две данные точки – ( А и В )– проходит единственная прямая (а ) (см. рисунок).
Из аксиом стереометрии: Через любые три точки, не лежащие на одной прямой, проходит единственная плоскость.
Через точки (А и В) лежащие на прямой ( а ), и через каждую точку ( b, c, d…..n ), не лежащую на этой прямой, проходит одна плоскость ( b, c, d…..n ). В пространстве точек, не лежащих на данной прямой. бесчисленное множество, следовательно, через две точки можно провести прямую и провести бесчисленное множество плоскостей.
Для наглядности можно представить себе сферу и плоскости сечения, проходящие через её диаметр и каждую точку на её поверхности.
№1.
Дано :
ΔАВС.
АВ = 20.
ВС = 7.
Sin(∠ABC) = 2/5.
Найти :
S(ΔАВС) = ?
Площадь треугольника равна половине произведения двух его сторон и синуса угла между ними.
В нашем случае -
S(ΔABC) = 0,5*АВ*ВС*sin(∠ABC)
S(ΔABC) = 0,5*20*7*(2/5)
S(ΔABC) = 70*(2/5)
S(ΔABC) = 140/5
S(ΔABC) = 28 (ед²).
28 (ед²).
№2.
Дано :
ΔАВС.
АВ = 15.
ВС = 8.
Sin(∠ABC) = 5/6.
Найти :
S(ΔАВС) = ?
Площадь треугольника равна половине произведения двух его сторон и синуса угла между ними.
Соответственно -
S(ΔABC) = 0,5*BC*АВ*sin(∠ABC)
S(ΔABC) = 0,5*8*15*(5/6)
S(ΔABC) = 60*(5/6)
S(ΔABC) = 300/6
S(ΔABC) = 50 (ед²).
50 (ед²).
Объяснение: