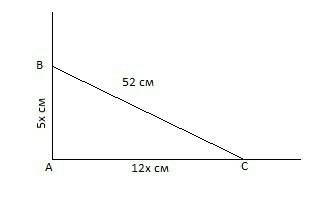
Построим прямой угол А и две материальные точки (В и С) которые движутся от тоски А со скоростью 5 см/с и 12 см/с. Расстояние между этими точками (ВС) будет являться гипотенузой треугольника АВС
Пусть время за которое между данными точками окажется расстояние равное 52 см будет равно х секунд, тогда пройденный путь (катеты АВ и ВС) 5х см и 12х см.
По теореме Пифагора: а^2+b^2=c^2 (где a и d катеты, c гипотенуза прямоугольного треугольника).
Подставим наши значения и решим полученное уравнение:
(5x)^2+(12x)^2=52^2
25x^2+144x^2= 2704
169x^2= 2704
x^2= 2704/169
x^2=16
x=√16
x1=-4
x2=4
Так как время не может быть отрицательным первый корень нам не подходит
ответ: через 4 секунды расстояние между точками будет равно 52 см.
Во-первых, заметим, что раз касательная касается окружности в точке С, то радиус, проведённый из С будет перпендикулярен касательной. Соответственно, радиус имеет длину R.
Обозначим проекции точек А и В на касательную соответственно А1 и В1. Тогда в прямоугольной трапеции А А1 В1 В внезапно обнаружим, что ОС является средней линией, потому что ОА = R, и ОВ также равно R. Раз такое дело, то радиус R является средним арифметическим оснований трапеции. Допустим, меньшее основание А А1 имеет длину х, тогда радиус R=2х, и большее основание В В1 = 3х.
Следовательно, продолжая гипотенузу АВ и касательную до пересечения (назовём точку пересечения буквой М) увидим, что АМ=R.
Далее применим теорему о секущей, которая скажет, что МС^2 = МА * МВ = R * 3R = 3*R^2. Отсюда МС = R * корень(3), то есть отношение МС/R = корень(3). По ходу, полученное отношение является тангенсом угла МОС, ибо угол МСО прямой. А тангенс какого угла равен корню(3) ? -- это угол 60 градусов, как нам известно из таблиц Брадиса.
Осталось последнее действие - заметить, что искомый угол В составляет половину от МОС, т.к.они опираются на одну и ту же дугу АС, но при этом АОС центральный, а В вписанный.
Итого, ответ: угол АВС = 60 / 2 = 30 градусов.
Ну, у меня так получилось.Лучше проверь за мной.