Пусть, большое основание трапеции равно х, тогда:
уравнение:
(х+15)/2=23
х+15=23*2
х+15=46
х=46-15
х=31
Объяснение:
См. Объяснение.
Объяснение:
Дано: KCl0₃ (хлорат калия, или бертолетова соль).
Задача 1.
Вычислите массовые доли химических элементов, входящих в состав хлората калия.
Решение.
1) Относительная молекулярная масса хлората калия:
39 + 35,5 + 3· 16 = 39 +35,5+48 = 122,5.
2) Массовая доля калия - это выраженное в процентах отношение его относительной атомной массы (39) к относительной молекулярной массе хлората калия:
39 : 122,5 · 100 = 31,84 %.
3) Массовая доля хлора - это выраженное в процентах отношение его относительной атомной массы (35,5) к относительной молекулярной массе хлората калия:
35,5 : 122,5 · 100 = 28,98 %.
4) Массовая доля кислорода- это выраженное в процентах отношение относительной атомной массы 3-х атомов кислорода (3·16=48) к относительной молекулярной массе хлората калия:
48 : 122,5 · 100 = 39,18 %.
Проверка:
31,84 + 28,98 + 39,18 = 100,00 %.
Задача 2.
Определите химическую формулу вещества и назовите это вещество, если известно, что в состав данного вещества входят 3 химических элемента, массовые доли которых составляют:
калия - 31,84 %,
хлора - 28,98 %,
кислорода - 39,18 %.
Решение.
1) Пусть в искомой формуле вещества:
а - количество атомов калия,
b - количества атомов хлора,
с - количество атомов кислорода.
2) Тогда относительная молекулярная масса (М) искомого вещества, выраженная через относительную атомную массу калия (39) и его массовую долю (0,3184), равна:
М = (39·а)/0,3184. (1)
Аналогично М можно выразить через хлор и кислород:
М = (35,5·b)/0,2898. (2)
М = (16·c)/0,3918. (3)
3) Приравнивая (1) и (2), находим :
11,3022а =11,3032b,
откуда а = b.
4) Приравнивая (1) и (3), находим:
15,2802а = 5,0944 с,
откуда с = 3а.
5) Таким образом, предполагаемая формула:
KCl0₃.
6) Делаем проверку (см. Задачу 1) и убеждаемся в том, что формула определена верно.
7) Делаем вывод:
формула искомого вещества - KCl0₃;
наименование вещества (согласно "Химической энциклопедии") - хлорат калия, или бертолетова соль.
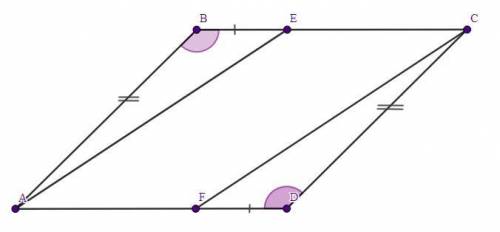
Четырёхугольник ABCD - параллелограмм.
ВЕ = DF (Е ⊂ ВС, F ⊂ AD).
Доказать :Четырёхугольник AECF - параллелограмм.
Доказательство :В параллелограмме противоположные углы и противоположные стороны равны между собой (свойство параллелограмма).Отсюда следует, что ∠В = ∠D, АВ = CD.
Рассмотрим ΔАВЕ и ΔCDF.
ВЕ = DF (по условию)
∠В = ∠D, АВ = CD (по выше сказанному) ⇒ ΔАВЕ = ΔCDF по двум сторонам и углу между ними (первый признак равенства треугольников).
Из равенства треугольников следует и равенство сторон АЕ и CF.
AD = BC (по свойству параллелограмма), но в своё очередь AD = BE + EC ; BC = DF + AF. Учитывая равенство из условия получаем, что ЕС = AF.
Если в четырёхугольнике противоположные стороны попарно равны, то этот четырёхугольник - параллелограмм (свойство параллелограмма).АЕ = CF ; ЕС = AF (по выше сказанному) ⇒ четырёхугольник AECF - параллелограмм.
ответ :Что требовалось доказать.
Средняя линия равна полусумме оснований.
Пусть большее основание равно х:
(х+15):2=23
х+15=23*2
х+15=46
х=46-15
х=31
Значит, большее основание равно 31
ответ: 31