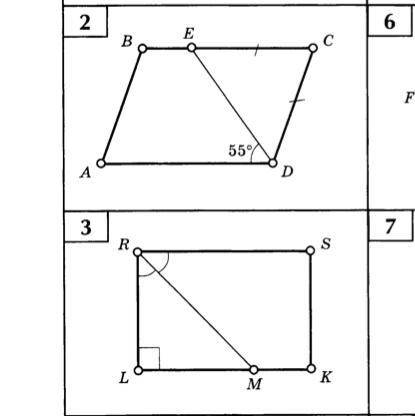
2)
55+55=110 МЫ НАШЛИ УГОЛ ADC
угол ABC=углу ADC
ADE=DEC
180-110=70
ECD=70
BCD=BAD
180-55=125=BED
3)
RLM=90
90:2=45=LRM=LMR
MRS=45
180-45=135=RMK
RSK=SKL=90
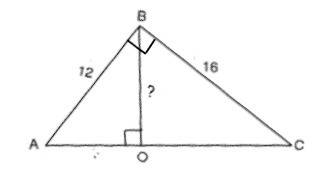
По т.Пифагора найдём гипотенузу.
АС=√(BC²+AC²)=√(256+144)=20 см
Высоту BO проще всего найти из площади треугольника.
S=BC•AB/2
S=BO•AC/2 Следовательно,
BC•AB=BO•AC, откуда
BO=BC•AB:AC
BO=16•12:20=9,6 см
-----
Вариант решения ( несколько длиннее) - его алгоритм дан ниже.
1) Находим гипотенузу по т.Пифагора
2) Катет прямоугольного треугольника – среднее пропорциональное между гипотенузой и проекцией этого катета на неё. ⇒
АВ²=АС•АО, ⇒ АО=АВ²:АС Отрезок СО находим вычитанием АО из гипотенузы или тем же что АО.
3) Высота прямоугольного треугольника, проведенная к гипотенузе, есть среднее пропорциональное между проекциями катетов на гипотенузу. ⇒
ВО²=СО•АО. Вычисления дадут ту же длину ВО=9,6 см
2.
ABCD - параллелограмм
BC || AD; ED - секущая, тогда
∠ADE=∠DEC=55°(внутренние накрест лежащие)
ΔECD - равнобедренный значит
∠DEC=∠EDC=55°
∠BED=180°-55°=125°(смежные)
∠DEC+∠EDC+∠C=180°(сумма всех углов треугольника)
55°+55°+∠C=180°, отсюда ∠C=70°
∠C=∠А=70°
∠А+∠B=180°(свойство параллелограмма)
70°+∠B=180°, значит ∠B=110°
∠B=∠D=110°
ответ: ∠DEC=∠EDC=55°;∠C=∠А=70°; ∠B=∠D=110°
3.
RM - биссектриса, значит
∠LRM=∠MRS=90°/2=45°
∠LMR=180°-(45°+90°)=45° (сумма всех углов треугольника)
ответ: ∠LRM=∠MRS=45°;∠LMR=45°;∠K=∠S=90°