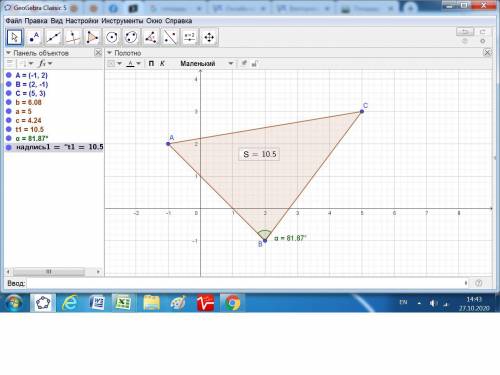
Даны точки А(-1;2), В(2;-1), С(5;3).
Вектор АВ = ((2-(-1)); (-1-2)) = (3; -3), модуль равен √(9+9) = √18 = 3√2.
Вектор АС = ((5-(-1); (3-2)) = (6; 1), модуль равен √(36+1) = √37.
cos a = (3*6 + (-3)*1) / (3√2*√37) = 15/(3√74) ≈ 0,58124.
Угол А = 54,46223°.
Угол В аналогично.
Вектор ВА -3 3 модуль 3√2
Вектор ВС 3 4 модуль 5
cos b = (-3*3 + 3*4) / (3√2*5) = 3/(15√2) ≈ 0,14142.
Угол B = 81,87°.
Площадь треугольника равна половине модуля векторного произведения.
Находим векторное произведение.
i j k| i j
AB 3 -3 0| 3 -3
AC 6 1 0| 6 1 = 0i + 0j + 3 k -0j - 0i + 18k = 21k.
S = (1/2)*21 = 10,5 кв.ед.
Объяснение:
"2. Один из углов, образованных при пересечении двух прямых, равен 63°. Найдите градусные меры остальных углов.
3. Один из смежных углов на 52° больше второго. Найдите эти углы.
4. На рисунке 265 AB =CD, А В C D E AC = CE. Докажите, что Рис. 265 BC = DE.
5. Углы АВС и свD смежные, луч Вм — биссектриса угла ABC Kyr ABM в 2 раза больший угол свD. Найдите углы ABC i CBD. Точки A, Bi слежат на одной прямой, AB = 15 см, отрезок Ас в 4 раза больше отрезка вс. Найдите отрезок АС. ответ: Объяснение: "2. Один из углов, образованных при пересечении двух прямых, равен 63°. Найдите градусные меры остальных углов. 3. Один из смежных угл"
2) При пересечении двух прямых образуются четыре угла: два смежных и два накрест лежащих.
Сумма смежных равна 180*, а накрест лежащие равны между собой.
Поэтому смежные углы: 180*-63*=117*, а вертикальные равны данным углам: один равен 63*, а другой - 117*
3) Пусть один из смежных углов равен х*. Тогда второй равен х+52*. Их сумма равна 180*.
х+х+52*=180*.
2х=128*.
х=64*. - меньший угол
Больший угол равен 64*+52=116*.
ответ: 64* и 116*.
4) Извините, но рисунка не наблюдаю... ???
5)