А1. ответ: 4.
А2. ответ: 4.
А3. ответ: 3.
А4. ответ: 1.
В1. Дано: ΔАВС, АВ = ВС = АС + 5 см, Р = 34 см.
Найти: АВ.
Решение: Пусть АС = х см, тогда АВ = ВС = х + 5,
x + (x + 5) + (x + 5) = 34
3x + 10 = 34
3x = 24
x = 8
АС = 8 см
АВ = ВС = 8 + 5 = 13 см
ответ: боковая сторона 13 см.
В2. Дано: ΔАВС, АВ = АС, АМ - медиана, Pabc = 40 см, Pabm = 33 см.
Найти: АМ.
Pabm = 33 см
АВ + ВМ + АМ = 33
2 · (АВ + ВМ + АМ) = 66
Так как АВ = АС, а ВМ = СМ, то
2АВ + 2ВМ + 2АМ = 66
АВ + АС + ВС + 2АМ = 66
2АМ = 66 - (АВ + АС + ВС) = 66 - Pabc = 66 - 40 = 16
AM = 16/2= 8 см
С1. 1) Если сумма равных сторон равна 26 см, то боковые стороны равны по 13 см, а основание - 10 см.
2) Обозначим боковые стороны а и b, основание - с.
а + с = 26 см
Рabc = 2а + с = 36 см
с = 36 - 2а
с = 26 - а
26 - a = 36 - 2a
a = 10 см
c = 16 см
ответ: 13 см, 13 см, 10 см или 10 см, 10 см, 16 см.
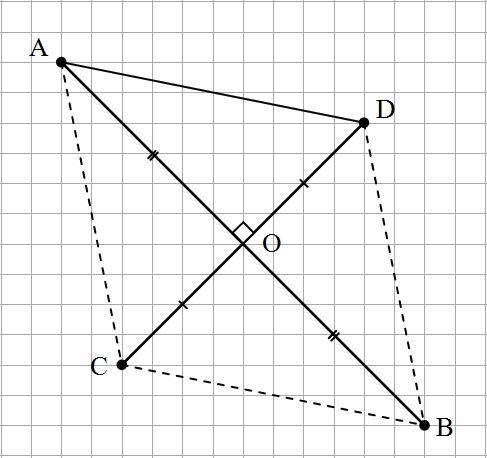
1). См. рис.1
По условию, т.О - середина отрезков АВ и СD.
Кроме того, AB⊥CD.
Четырехугольник, в котором диагонали пересекаются под прямым углом и делятся точкой пересечения пополам, является ромбом.
Следовательно, AD = DB = BC = CA = 17 (см)
В ΔАОD и ΔСОB:
АО = ОВ; СО = ОD; ∠АОD = ∠COB = 90°
Следовательно, прямоугольные треугольники ΔАОD и ΔСОB равны по двум катетам.
---------------------------------
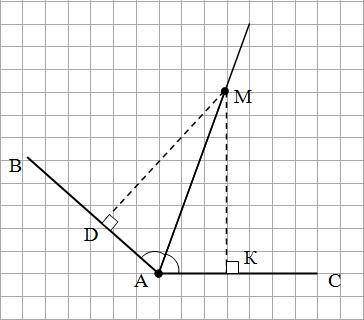
2). См. рис.2
В ΔADM и ΔАКМ:
∠ADM = ∠AKM = 90°
∠DAM = ∠KAM = 70° (АМ - биссектриса ∠ВАС)
Тогда:
∠DMA = ∠KMA = 180 - (90 + 70) = 20°
Следовательно, прямоугольные треугольники ΔADM и ΔАКМ равны по общей гипотенузе и острому углу.
--------------------------------
3). В ΔАВЕ и ΔDCE:
∠ABE = ∠DCE = 90°
∠BEA = ∠CED, как вертикальные
Тогда:
∠ВАЕ = ∠СDE = 20°
и ∠BEA = ∠CED = 180 - (90 + 20) = 70°
Так как ∠ВАЕ = ∠СDE = 20° и АВ = СD, то:
ΔABE = ΔDCE по катету и прилежащему острому углу.
Величина угла ∠АЕD:
∠АЕD = 180 - 70 = 110°
В ΔАЕD:
AE = ED, как гипотенузы в равных треугольниках.
Следовательно, ΔАЕD - равнобедренный и:
∠EAD = ∠EDA = (180 - 110) : 2 = 35°
В ΔABD и ΔACD:
∠BAD = ∠CDA = 20 + 35 = 55°
и АВ = CD
Тогда:
ΔABD = ΔACD по катету и прилежащему острому углу.
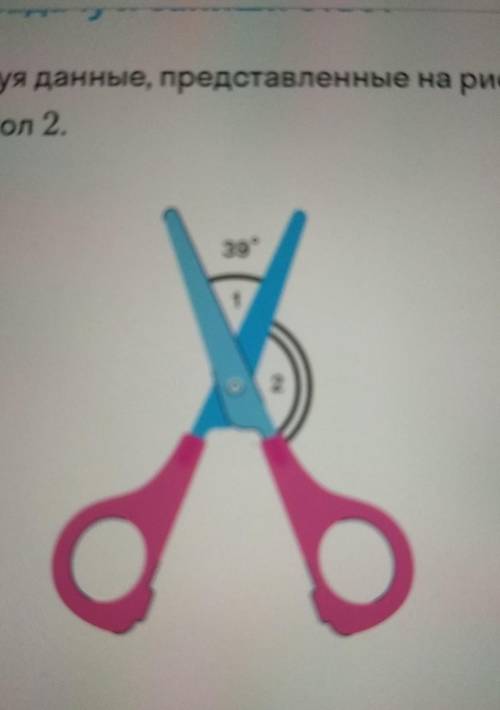
там 39 ?
Объяснение:
если 39 то 1 ый и 2 ой смежные углы
их сумма равна 180 тогда
180-39=141 градуса