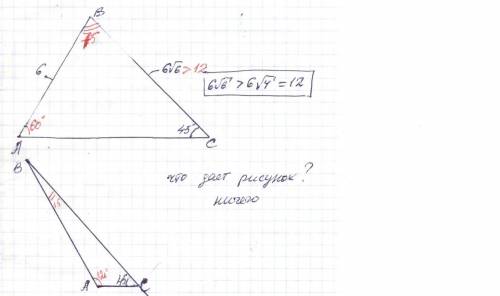
Найдите углы A и B треугольника ABC, если AB=12 см, BC=6√6 см, угол C= 45°.
ответ: 60° , 75° или 120° , 15° .
Объяснение:
По теореме синусов : BC / sin(∠A) =AB / sin(∠C ) ⇔
6√6/sin(∠A)=12/sin45°⇔sin(∠A) =6√6*sin45°/12=6√6 *(√2/2) / 12 = 3 /2 ⇒
∠A= 60° или ∠A= 120° . Оба верны ∠A > ∠C , т.к. BC > AB
( в треугольнике против большой стороны лежит большой угол )
* * * BC > AB : BC = 6√6 > 6√4 = 12 = AB * * *
∠B = 180° - (∠A+√C) → ∠B = 75° или ∠B = 15° см. лишнее приложение
сторону квадрата можно найти зная его диагональ (сторона равна диагональ /V2) или а-СК/V2 2) диагональ квадрата - бисектриса угла С, а в силу того что треугольник равнобедренный, то и медиана, а то что медиана прямоугольного треугольника проведеная к гипотенузе равна половине гипотенузы - известный факт. Таким образом диагональ квадрата 3D гипотенуза/2 или СК-АВ/2 3) гипотенуза равнобедренного прямоугольного треугольника равна катет*V2 или АВ-АС*V2-BC"V2 Вычисляем: 3 АВ-12 V2 (см) 3+2 > СК-12 /2/2-6V2(см) 3+2+1> а-(6 w2)/(V2)-6 (см)
Без того знака не знаю