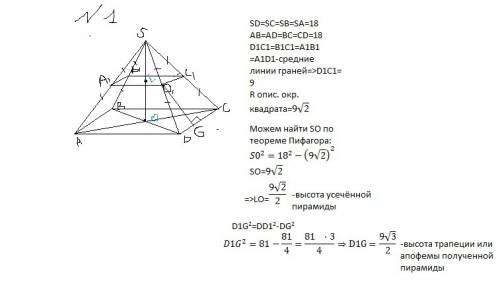
Боковая поверхность правильной усеченной пирамиды равна произведению полусуммы периметров оснований на апофему:
Sбок=1/2(p1+ p2) a
где р1 и р2 - периметры оснований, а- апофема ( высота боковой грани)
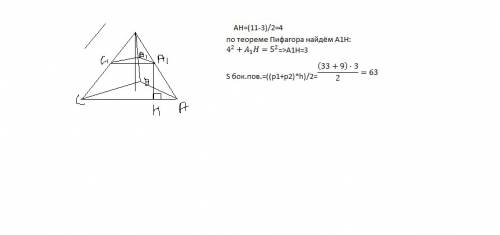
Полусумму периметров оснований найти очень просто. Каждое из них имеет 3 стороны, поэтому
3·(3+11):2= 42:2=21 см
Боковая грань правильной усеченной пирамиды - равнобедренная трапеция.
Апофему найдем по теореме Пифагора из треугольника, в котором боковаое ребро - гипотенуза, апофема и полуразность оснований трапеции - катеты.
h²=5² -( (11-3):2)²=5²-4²=9
h=√ 9=3 см
Sбок=21·3=63 см²
Объяснение:
М(4;-3) ; а) відстань від точки М(4;-3) до осі OX : | - 3 | = 3 ;
б) відстань від точки М(4;-3) до осі OY; | 4 | = 4 ;
в) відстань від точки М(4;-3) до початку координат знайдемо за
теоремою Піфагора : ОМ = √ ( 4² + (- 3 )² ) = √25 = 5 .