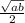, высота трапеции: h=2r=
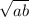=√8=2√2
ответ:
дана прямая а и точка м, не лежащая на ней.
проводим дугу с центром в точке м (черная), произвольного радиуса, большего расстояния от точки м до прямой.
получили две точки пересечения дуги и прямой а. обозначим их а и в.
теперь построим две окружности (красных), с центрами в данных точках, произвольного одинакового радиуса (большего половины отрезка ав).
точки пересечения этих окружностей назовем к и н.
проводим прямую кн.
кн - искомый перпендикуляр к прямой а.
доказательство:
если точка равноудалена от концов отрезка, значит она лежит на серединном перпендикуляре к отрезку.
ак = кв как равные радиусы, значит к лежит на серединном перпендикуляре к отрезку ав.
ан = нв как равные радиусы, значит н лежит на серединном перпендикуляре к отрезку ав.
кн - серединный перпендикуляр к отрезку ав.
ма = мв как равные радиусы черной окружности, значит и точка м лежит на прямой кн, т.е. перпендикуляр к прямой а проходит через точку м.
получившийся треугольник PAD в любом случае будет равнобедренным (по условию) и угол APD = ADP = 10 градусов. PAD = 160 градусов.
второй получившийся треугольник PAB тоже в обоих случаях будет равнобедренным...
в одном случае остроугольным PAB = PAD - 90 = 160-90 = 70
APB=PBA = (180 - PAB)/2 = 110/2 = 55
во втором случае тупоугольным PAB = 360 - PAD - 90 = 360-160-90 = 110
APB=PBA = (180 - PAB)/2 = 70/2 = 35