
5)точка O лежит на биссектрисе угла A так как точка O равноудалена от прямых AB и AC => ∠BAO=CAO=30°
∠OBA прямой => AO=2OB=5*2=10
AK=AO-KO=10-5=5
ответ 5
-----------------
6)AK=KC=3 так-как окружность лежит в точке пересечения биссектрис, а биссектриса равнобедренного треугольника опущенная к основанию является медианой и высотой поэтому радиус OK лежит на биссектрисе угла B и делит AC напополам.
AK=AM=3; KC=CN=3 и BN=BM=5 как отрезки касательных.
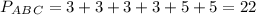
ответ 22
------------------
7)В прямоугольном треугольнике радиус вписанной окружности можно высчитать по формуле:
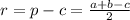
где p полупериметр,а (c) гипотенуза. (эта формула очень просто выводится из отрезков касательных, можешь сам попробовать ее вывести)
подставляем числа:
r=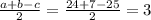
ответ: 3
28 + 4√97; 60°
Объяснение:
1. Пусть неизвестная сторона параллелограмма равна х см. Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон, тогда:
12² + 32² = 28(14² + х²), откуда х² = 388. Тогда периметр параллелограмма равен 2*14 + 2√388 = 28 + 4√97.
2. Пусть острый угол между диагоналями параллелограмма равен α. Косинус острого угла между диагоналями параллелограмма равен отношению разности квадратов сторон параллелограмма к произведению его диагоналей, тогда:
cosα = (х² - 14²)/(12*32) = (388 - 196)/(12*32) = 1/2, и α = 60°
Объяснение:
KN= 4,6
NM= 9,7