Дан треугольник abc. ав-основание-12. медианы ам и вк-пересекаются в точке о угол аов-120 градусов. - id204404920200520 от aArisha2772 20.05.2020 01:54

Question

Геометрия: Дан треугольник abc. ав-основание-12. медианы ам и вк-пересекаются в точке о угол аов-120 градусов. найти медины

aArisha2772 · Accepted Answer

1) ΔAOC = ΔBOC по двум катетам (OC - общий, AO = OB т.к. O - середина AB) ⇒ CB = AC = 10

ответ: 10

2) В равнобедренном треугольнике углы при основании равны ⇒ ∠ABC = ∠ACB = (180 - 80)/2 = 50°

ответ: 50°

3) ∠CAB смежный с углом ∠BAK ⇒ ∠CAB = 180 - 120 = 60°

Рассмотрим ΔABC - прямоугольный

∠CAB = 60° ⇒ ∠ABC = 90 - 60 = 30°

Катет, лежащий напротив угла в 30° равен половине гипотенузы: AC = 1/2 AB

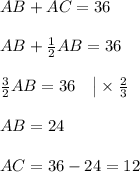
$AB + AC = 36\\ \\ AB + \frac{1}{2}AB = 36\\ \\ \frac 3 2 AB = 36~~~\big |\times \frac 2 3 \\ \\ AB = 24 \\ \\ AC = 36 - 24 = 12$

ответ: 12

4) В четырёхугольнике ABCD диагонали пересекаются и точкой пересечения делятся пополам ⇒ ABCD - параллелограмм

В параллелограмме сумма углов, прилежащих к одной стороне, равна 180°

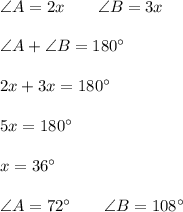
$\angle A = 2x\qquad \angle B = 3x \\ \\ \angle A + \angle B = 180^\circ \\ \\ 2x + 3x = 180^\circ \\ \\ 5x = 180^\circ\\ \\ x = 36^\circ \\ \\ \angle A = 72^\circ \qquad \angle B = 108^\circ$

ответ: 72°

1.через середину отрезка ав проведена прямая см, пересекающая его в точке о под углом 90°.известно,

Дан треугольник abc. ав-основание-12. медианы ам и вк-пересекаются в точке о угол аов-120 градусов. найти медины

MOGZ ответил