ответ: 8√2π см
Объяснение:
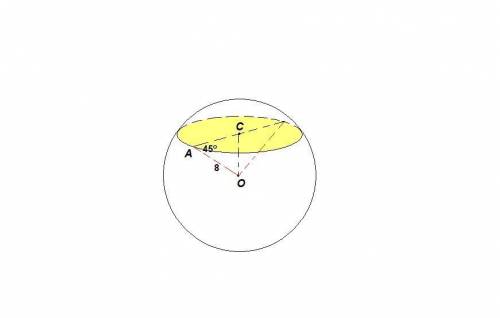
О - центр сферы, ОА = 16 / 2 = 8 см - радиус сферы.
Сечение сферы - окружность, С - центр сечения, СА - радиус сечения.
Длина линии пересечения сферы плоскостью - длина этой окружности.
Отрезок, соединяющий центр сферы с центром сечения, перпендикулярен плоскости сечения, тогда СА - проекция наклонной ОА на плоскость сечения, значит угол между радиусом и его проекцией на плоскость ∠ОАС = 45°.
ΔОСА: ∠ОСА = 90°,
cos 45° = CA / OA
CA = OA · cos 45° = 8 · √2/2 = 4√2 см
Длина окружности сечения:
C = 2π · CA = 2π · 4√2 = 8√2π см
варианте) и на полученной второй его стороне откладываем отрезок
АВ, равный данной гипотенузе. Из точки В опускаем перпендикуляр на
прямую "а". Для этого:
Из точки В проводим окружность любого радиуса R, чтобы пересекла
прямую "а" в точках G и Q. Из точек G и Q тем же радиусом проводим
две дуги, пересекающиеся в точке M. Прямая ВМ - искомый перпендикуляр.
На пересечении прямых ВМ и "а" ставим точку С.
Соединяем точки А,В и С и получаем прямоугольный треугольник АВС
с прямым углом <C и с заданными гипотенузой и острым углом.
2. На прямой "а" откладываем отрезок, равный одной из сторон, например, АС. Проводим окружности с центрами в точках А и С радиусами, равными двум другим сторонам, например, АВ и СВ соответственно. В точке пересечения этих окружностей получаем точку В. Треугольник построен.
3. На прямой "а" откладываем отрезок, равный стороне АВ, к которой проведена высота СН. Проводим окружность радиуса ВС с центром в точке В. Из точки В к прямой "а" восстанавливаем перпендикуляр и на нем откладываем отрезок ВР, равный высоте СН. Из точки Р проводим перпендикуляр к отрезку ВР и в точке пересечения этого перпендикуляра с проведенной ранее окружностью ставим точку С.
Соединив точки А,С и В получаем искомый треугольник.
P.S. Построение перпендикуляра к прямой в заданную точку не описываю - это стандартное построение.