R ⊥ BD = 0
Объяснение:
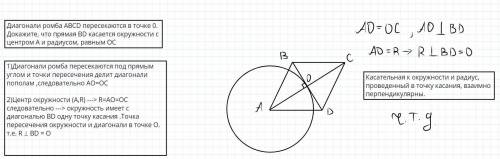
1. Диагонали ромба пересекаются под прямым углом и точки пересечения делит диагонали пополам (по свойству),следовательно AO=OC ⇒
⇒ 2. Центр окружности (А,R) ---> R=AO=OC следовательно ---> oкружность имеет с диагональю BD одну точку касания .Точка пересечения окружности и диагонали в точке О.
т.е. R ⊥ BD = О
т.к. касательная BD к окружности и радиус, проведенный в точку касания, взаимно перпендикулярны.
Касательная к окружности — это прямая, имеющая с ней всего одну общую точку О.
Р(ΔNKP) = 56 см
Объяснение:
Так как A – середина NK, B – середина KP, C – середина NP, то АВ, ВС, АС - средние линии ΔNKP.
Средняя линия треугольника — отрезок, который соединяет середины двух сторон.Средняя линия треугольника параллельна третьей стороне треугольника, а длина средней линии треугольника равна половине этой стороны.Следовательно:
АВ = 1/2 * NP,
ВС = 1/2 * NK,
АС = 1/2 * KP.
Отсюда:
NP = 2*АВ = 2*7 = 14 см
NK = 2*ВС = 2*9 = 18 см
KP = 2*АС = 2*12 = 24 см
Периметр треугольника - это сумма всех его сторон.
Р(ΔNKP) = NP + NK + KP = 14+18+24 = 56 см

Объяснение:
Пусть разностью векторов 2С и p будет вектор n. 2С {2×2;-5×2} , значит 2С{4;-10}
2С{4;-10} -p {-3;1}, следовательно вектор n
{7;-11}