S = 4(7√3+6) см²
Р = 22+4√3(1+√2) см.
Объяснение:
АВCD - трапеция. Опустим высоты ВН и СР на основание AD. В прямоугольном треугольнике АВН катет АН лежит против угла 30° (по сумме острых углов прямоугольного треугольника) и равен половине гипотенузы АВ. Второй катет ВН найдем по Пифагору: ВН=√(АВ²-АН²). Тогда
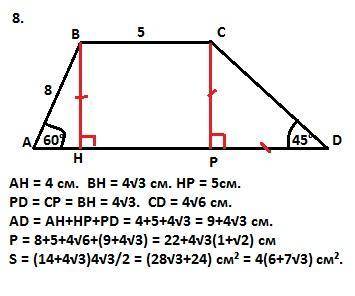
АН = 4 см. ВН = √(8²-4²) = 4√3 см.
CР = ВН (высота трапеции) => PD = CР (как катеты равнобедренного прямоугольного треугольника (острые углы равны по 45° - дано).
CD = √(2·BH²) = 4√6 см. (по Пифагору).
AD = AH+HP+PD = 4+5+4√3 = (9+4√3) см.
Тогда S = (BC+AD)·BH/2 = (14+4√3)·4√3/2 = (28√3 + 24)см²
Периметр Р = 8+5+4√6+(9+4√3) = 22+4√3(1+√2) см.
Призма
Призмой называется многогранник, две грани которого n-угольники, а остальные n граней — параллелограммы.Боковые ребра призмы равны и параллельны.
Перпендикуляр, проведенный из какой-либо точки одного основания к плоскости другого основания, называется высотой призмы. Отрезок, соединяющий две вершины призмы, не принадлежащие одной грани, называется диагональю призмы.Поверхность призмы состоит из оснований и боковой поверхности призмы. Боковая поверхность призмы состоит из параллелограммов.
Если боковые ребра призмы перпендикулярны к основаниям, то призма называется прямой. В противном случае призма называется наклонной.
У прямой призмы боковые грани – прямоугольники.
Высота прямой призмы равна ее боковому ребру.
Прямая призма называется правильной, если она прямая, и ее основания — правильные многоугольники
Площадь поверхности и объём призмы
Пусть H — высота призмы, — боковое ребро призмы, — периметр основания призмы, площадь основания призмы, — площадь боковой поверхности призмы, — площадь полной поверхности призмы, - объем призмы, — периметр перпендикулярного сечения призмы, — площадь перпендикулярного сечения призмы. Тогда имеют место следующие соотношения:
Для прямой призмы, у которой боковые ребра перпендикулярны плоскостям оснований, площадь боковой поверхности и объем даются формулами:
Параллелепипед
Параллелепипедом называется призма, основанием которой является параллелограмм.
Параллелограммы, из которых составлен параллелепипед, называются его гранями, их