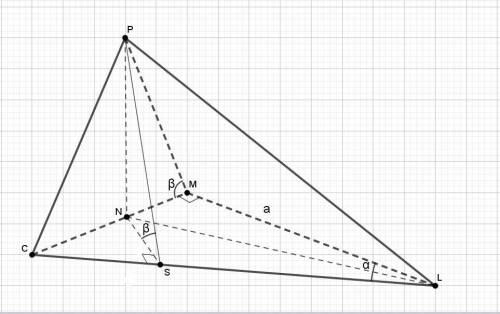
Так как две грани одинаково наклонены к основанию, то проекция ребра PL на основание - это биссектриса угла α.
Отрезок MN = a*tg(α/2).
Высота РН = a*tg(α/2)/ tg(β).
Боковое ребро РМ - оно же и высота боковой грани PML - равно:
РМ = MN / cos(β) = a*tg(α/2)/cos(β).
Катет основания СМ = a*tg(α).
Гипотенуза CL = a/cos(α).
Высота PS грани CPL равна длине ребра РМ по равенству их проекций: MN = NS.
Теперь можно определить площади боковых граней.
S(CPM) = (1/2)(a*tg(α))* a*tg(α/2)/ tg(β) = (a²/2)*tg(α)*tg(α/2)/ tg(β).
S(PML) = (1/2)a*(a*tg(α/2)/cos(β)) = (a²/2)*tg(α)*tg(α/2)/cos(β).
S(CPL) = (1/2)(a/cos(α))* (a*tg(α/2)/cos(β)) = (a²/(2cos(α))*(tg(α/2)/cos(β)).
Осталось сложить:
Sбок = (a²/2)((tg(α/2)/tg(β))+ (tg(α/2)/cos(β)) + (tg(α/2)/(cos(α)*cos(β))).
Дано: СВ = a, ∟A = а, ∟C = 90°.
Побудувати: ∆АВС: ∟C = 90°, СВ = а, ∟A = а.
Побудова:
1) Відкладемо СВ = а.
2) Побудуємо ВК ┴ СВ.
3) Відкладемо ∟XBE = ∟A = а.
4) Побудуємо CF ┴ СВ.
5) CF i ВЕ перетинаються в т. А.
6) ∟KBA = ∟CAB = а як різносторонні при СА ‖ ВК i січній ВА.
7) ∆ВС - шуканий.
Объяснение:Дано: СВ = a, ∟A = а, ∟C = 90°.
Побудувати: ∆АВС: ∟C = 90°, СВ = а, ∟A = а.
Побудова:
1) Відкладемо СВ = а.
2) Побудуємо ВК ┴ СВ.
3) Відкладемо ∟XBE = ∟A = а.
4) Побудуємо CF ┴ СВ.
5) CF i ВЕ перетинаються в т. А.
6) ∟KBA = ∟CAB = а як різносторонні при СА ‖ ВК i січній ВА.
7) ∆ВС - шуканий.
ответ: 1. 1) бағытталған
c, d
2) коллинеарлы
с, д
3) қарама-қарсы
a, b; c, e
Объяснение: