Дан прямоугольный треугольник с катетами а и b.
Доказать: S = ab/2
Доказательство:
Площадь любого треугольника равна половине произведения стороны на проведенную к ней высоту.
b - сторона, высота, проведенная к ней, совпадает с катетом а, значит
S = 1/2 ba
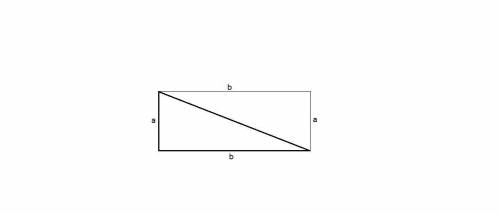
Достроим прямоугольник на катетах а и b как на сторонах.
Гипотенуза треугольника является диагональю прямоугольника и делит его на два равных треугольника.
Площадь прямоугольника равна произведению сторон:
Sпрям = ab,
тогда площадь прямоугольного треугольника равна ее половине:
Sтр = ab/2
Объяснение:
Чтобы найти периметр,нужно додать каждую сторону. По условию задачи АВ=CD=5см
Соответственно АD=ВС=10 см
Р=5+5+10+10=30 см.