Дано :
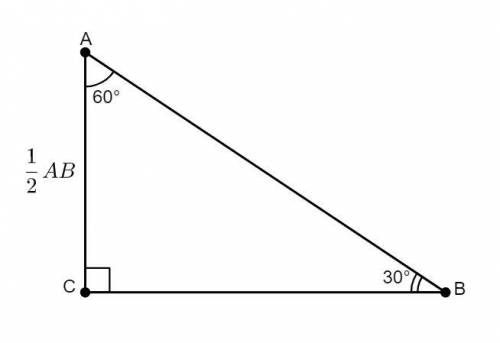
ΔАВС — прямоугольный (∠С = 90°).
∠А = 60°.
АВ + короткий катет = 9 см.
Найти :
∠В = ?
Короткий катет = ?
В прямоугольном треугольнике сумма острых углов равна 90°.Следовательно, ∠А + ∠В = 90° ⇒ ∠В = 90° - ∠А = 90° - 60° = 30°.
В треугольнике против меньшего угла лежит меньшая сторона.Так как ∠В — самый меньший угол в ΔАВС, то АС (катет, лежащий напротив этого угла) самая меньшая сторона, соответственно и есть короткий катет.
Тогда нам нужно найти АС.
В прямоугольном треугольнике против угла в 30° лежит катет, равный половине гипотенузы.Следовательно, АС =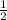 
*АВ или АВ = 2*АС.
Составим уравнение —
АВ + АС = 9 см
2*АС + АС = 9 см
3*АС = 9 см
АС = 3 см.
30° ; 3 см.
2. Отрезки касательных к окружности , проведенных из одной точки , равны и составляют равные углы с прямой , проходящей через эту точку и центр окружности.
Для начала найдём длину боковой стороны CD
Найдём её из прямоугольного треугольника COD (∠COD=90° по условию)
Соединим теперь точку О с точками касания окружности со сторонами АВ и BD . По теореме, углы между радиусами этой окружностью и сторонами будут равны 90 градусов.
Получаем Четырехугольник OKAM две смежные стороны которого равны , а значит этот четырехугольник квадрат . (Три его угла равны 90 градусов, А - по условию, значит четырехугольник прямоугольный)
Теперь рассмотрим треугольник MOD
Он прямоугольный.
Тк как его гипотенуза OD равна 20 см, а катеты равны а и d , то
Углы СDО и ODA равны по теореме. Значит имеем два подобных прямоугольных треугольника (по двум углам) ΔCOD и ΔDOM
Из подобия треугольников имеем:
Но
Из системы уравнений получаем:
а=12
d=16
c+d=25
c=9
Теперь рассмотрим ещё один четырехугольник KOPB
Аналогично доказываем, что он квадрат. Но, одна из его сторон равна а, значит b=a=12⇒