
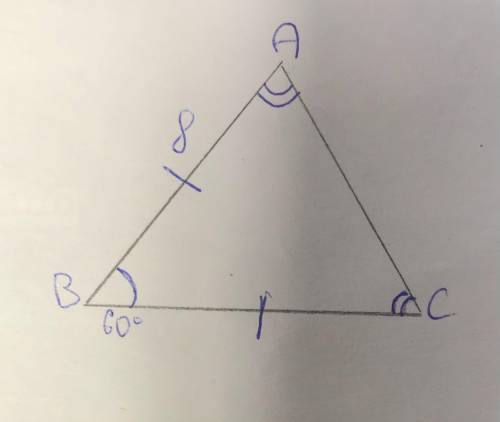
AC=8; BC=8
Объяснение:
1)При данных условиях B можно взять за вершину р/б(равнобедренного) треугольника и тогда мы получим:
Дано:
ΔBAC - р/б
AC - основание
BA = BC
∠B = 60°
2)т.к. ΔBAC - р/б , то углы прилегающие к его основанию - равные ⇒ ∠A = ∠C
3)градусная мера треугольника - 180 ° ,а исходя из этого можно сделать такие исчисления:
3)1)180 - 60 = 120 ° - ∠A+∠C
3)2)т.к. углы A и C равны ⇒ 120 : 2 =60°- ∠A=∠C
3)3)из этого мы видим ,что все углы треугольника равны,а значит и все его стороны равны,обозначаем треугольник как р/с (равносторонний) и получаем что AB = AC = BC ⇒ 8 = 8 = 8
Дано:
ΔАВС
окр. (О; ОС)
дуга ВС : дуга АС : дуга АВ = 3 : 7 : 8
ВС = 20
Найти: ОС.
Пусть k - одна часть, тогда дуга ВС = 3k, дуга АС = 7k, дуга АВ = 8k. Т.к. в окружности 360°, то составим и решим уравнение:
3k + 7k + 8k = 360;
18k = 360;
k = 20.
Найдем дугу ВС: дуга ВС = 3 * 20 = 60°.
∠ВОС - центральный, опирается на дугу ВС, значит ∠ВОС = 60°.
ΔВОС - равнобедренный, т.к. ОВ = ОС (радиусы), по свойству углов в равнобедренном треугольнике ∠ОВС = ∠ОСВ = (180° - ∠ВОС) : 2 = (180° - 60°) : 2 = 60°.
Следовательно, ΔВОС - равносторонний и ОС = ОВ = ВС = 20.
ответ: 20.
Объяснение:
Отрезок BD - диаметр окружности с центром О. Хорда AC делит
пополам радиус OB и перпендикулярна к нему. Найдите углы
четырёхугольника ABCD и градусные меры дуг AB BC CD и AD.
Соединим центр окружности с вершиной А.
Отрезок ОА - радиус, МО равен его половине.
sin ∠ МАО равен МО: АО=1/2.
Это синус 30°∠ МАО=30°, ⇒∠ АОВ=60°.
ВО=АО=радиус окружности. ⇒ △ АОВ равнобедренный.
Сумма углов треугольника 180 градусов.
∠ ОВА=∠ОАВ=(180°-60°):2)=60° ⇒ △ АОВ- равносторонний.
Углы ВАD и ВСD опираются на диаметр ⇒ они прямые=90°.
⊿ ВСD и ⊿ВАD -прямоугольные, и
∠СDВ=∠АDВ=180°-(90°-60°)=30°
⊿ ВСD=⊿ВАD.
∠ D=2 ·∠АDВ=2·30°=60°
Сумма углов четырехугольника 360°
∠АВС=360°- 2·90°- 60°=120°
Градусная мера дуги равна центральному углу, который на нее
опирается.
На дугу АВ опирается центральный угол АОВ=60°⇒ ее градусная мера 60°
На дугу СВ опирается центральный угол СОВ=60°⇒ ее градусная мера 60°
В треугольнике САD ∠САD=∠DАС=60°
Вписанный угол равен половине градусной меры дуги, на которую
опирается.
На дугу CD опирается вписанный угол САD=60°⇒ она равна 2·60°=120°
На дугу АD опирается вписанный угол АСD=60°⇒ она равна 2·60°=120°
∠А=С=90°
∠В=120°
∠Д=60°
градусные меры дуг
AB=60°
BC=60°
CD=120°
AD=120°.
BC=8, AC=8
Объяснение:
В треугольнике АВС стороны АВ и ВС равны, значит, этот треугольник равнобедренный, причем АС - основание. В равнобедренном треугольнике углы при основании равны. Значит, угол А равен углу С.
В треугольнике сумма всех углов равна 180 градусов. Поскольку угол В равен 60 градусов, то на углы А и С остается 120 градусов, а раз они равны, то каждый из них равен 120/2=60 градусов. Получаем, что в треугольнике все углы равны 60 градусов, а значит, что этот треугольник равносторонний, т.е. все стороны равны между собой и равны 8.