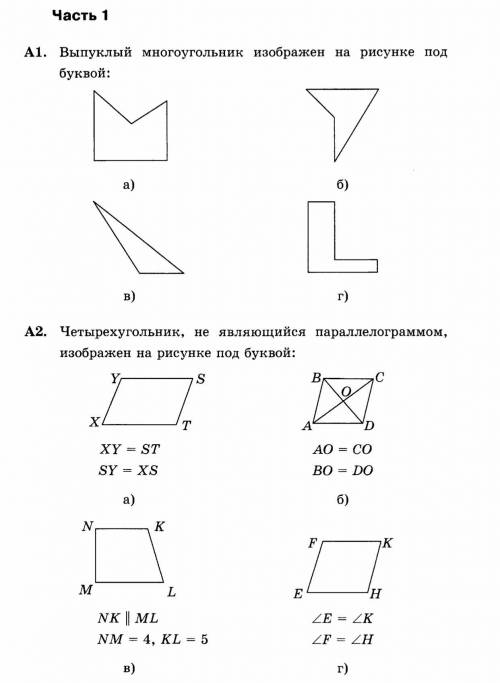
А1: в)
А2: в)
Объяснение:
Выпуклым многоугольником называется многоугольник, в которому для любых двух точек многоугольника отрезок, их соединяющий полностью принадлежит многоугольнике. В А1 вариант г) не подходит точно, потому что если соединить точки, то там один отрезок будет лежать вне фигуры.
Параллелограмм ето четырехугольник, у которого противоположные стороны параллельны. В А2 подходят все варианты, кроме в), потому что ето трапеция.
пусть х - одна часть
Тогда один из катетов - это 5х, другой - 6х
составим уравнение
25x² + 36x² = 14641
61x² = 14641
x²=14641/61
x=√14641/61=121/√61
Тогда один катет будет 605/√61, второй катет - 726/√61
Теперь найдем отрезки. Так как из прямого угла проведена к гипотенузе высота, то катет прямоугольного треугольника есть среднее проворциональное для гипотенузы и отрезка гипотенузы, заключенного между катетом и высотой, проведенной из вершины прямого угла
пусть один из отрезков гипотенузы = а
Второй отрезок = b
Гипотенуза - с
берем первый катет и первый отрезок
(605/√61)² = с * а
(605/√61)² = 121а
366025/61 = 121а
а = 3025/61
найдем b. По аналогии:
(726/√61)² = с * b
(726/√61)² = 121b
b = 4356/61
А1) г А2) а