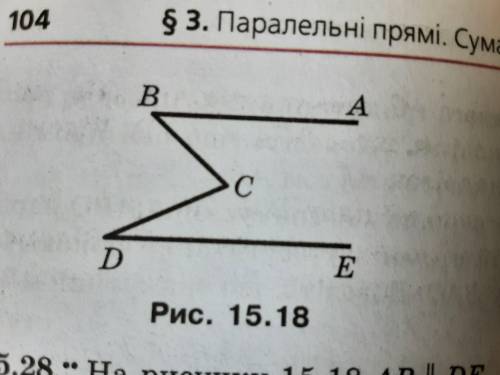
Пусть катеты равны а и b, гипотенуза равна с и высота, проведённая из вершины прямого угла, равна h.
Высота прямоугольного треугольника, проведённая из вершина прямого угла к гипотенузе, равна произведению катетов, делённому на гипотенузу прямоугольного треугольника.Гипотенузу треугольника найдём по теореме Пифагора (сумма квадратов катетов равна квадрату гипотенузы) :
c² = a² + b² = 5² + 12² = 25 + 144 = 169
c = √c² = √169 = 13 см.
Тогда, по выше сказанному, h равно :
h = ab / c = 5 см*12 см / 13 см = 60 см²/13 см = 4 8/13 см.
4 8/13 см.
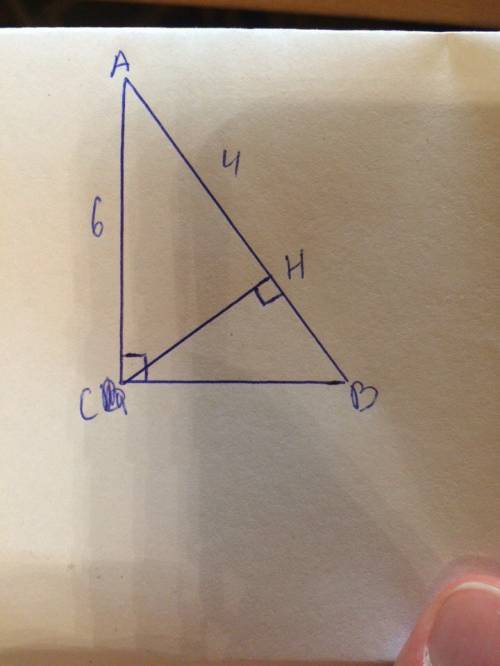
Изучали же уже теорему об углах, образованных двумя параллельными прямыми и секущей? Односторонние, внутренние накрест лежащие, внешние накрест лежащие, соответственные углы.
Нужно доказать, что
BCD = ABC + CDE.
Начнём, проведём прямую BD. Так как AB || DE, то BD будет секущей двух параллельных прямых AB и DE. И для углов, образованных этими тремя прямыми, действуют свойства углов при параллельных прямых и секущей. => ABD и BDE — внутренние односторонние углы. Воспользуемся свойством «сумма внутренних односторонних углов при параллельных прямых и секущей равна 180°» => ABD + BDE = 180°.
Рассмотрим треугольник BCD. Сумма углов в треугольнике равна 180°
=> BCD + BDC + CBD = 180°,
=> BCD = 180° – BDC – CBD.
Итак, собираем всё вместе:
ABD + BDE = 180°;
BCD = 180° – BDC – CBD.
И добавим, что:
ABD = ABC + CBD, CBD = ABD – ABC;
BDE = BDC + CDE, BDC = BDE – CDE;
Теперь объединяем:
BCD = 180° – BDC – CBD = 180° – (BDE – CDE) – (ABD – ABC) = 180° – BDE + CDE – ABD + ABC = 180° – (ABD + BDE) + CDE + ABC = 180° – 180° + CDE + ABC = CDE + ABC
Что и требовалось доказать:
BCD = ABC + CDE