
ответ: 6√5 см
Объяснение:
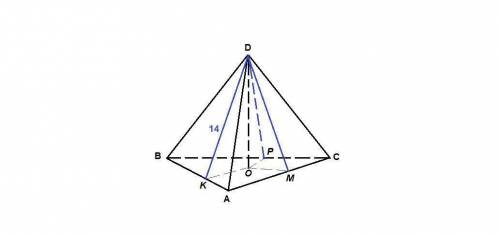
Пусть DO - высота пирамиды, DK, DM, DP - высоты боковых граней.
DK = DM = DP = 14 см по условию.
OK, OM и ОР - проекции наклонных, тогда они перпендикулярны сторонам треугольника АВС по теореме о трех перпендикулярах.
Если равны наклонные, проведенные из одной точки, то равны и их проекции, значит
ОК = ОМ = ОР, следовательно О - центр окружности, вписанной в ΔАВС, а ОК, ОМ и ОР - ее радиусы.
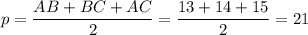
По формуле Герона
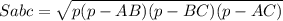
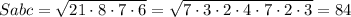 см²
см²
S = pr
84 = 21r
r = 4 см
ΔDKO: ∠DOK = 90°
по теореме Пифагора
DO = √(DK² - KO²) = √(196 - 16) = √180 = 6√5 см
6 ед.
Объяснение:
Пусть х будет одна сторона, тогда другая сторона будет (х+2).
Площадь это произведение длины на ширину.
Составляем уравнение.
х(х+2)=24
х²+2х-24=0
а=1
b=2
c=-24
D=b²-4ac=2²-4*1*(-24)=4+96=100
X1=(-b+√D)/2a=(-2+√100)/2*1=(-2+10)/2=4 ед. сторона прямоугольника.
Х2=(-b-√D)/2a=(-2-10)/2=-12/2=-6 число отрицательное не подходит.
Одна сторона х=4. Другая х+2. Подставим значение х.
4+2=6 ед. другая сторона прямоугольника.
ответ:6 большая сторона прямоугольника.
Проверка
6*4=24 ед² площадь прямоугольника.