Объяснение:
Если точки лежат на одной прямой, то длина большего отрезка должна быть равна сумме длин меньших отрезков. Проверим:
12 = 5 + 8
12 = 13 - неверно,
значит точки M, N и Р не лежат на одной прямой.
Объяснение:
Чтобы найти площадь сечения, которое является кругом, нужно знать его радиус r. Найдем его, рассмотрев сечение шара плоскостью, перпендикулярной искомому сечению (тому, площадь которого мы должны найти). (Смотри рисунок.)
Рассматриваемое сечение - тоже круг, его центр О совпадает с центром шара, а радиус R = 25 см. Проведем хорду АВ. Это - диаметр искомого сечения. Расстояние до него - длина перпендикуляра, опущенного на АВ из точки О (обозначим его ОН). Длина этого перпендикуляра h = 20 см. Получился прямоугольный треугольник ОАН с гипотенузой R и катетами h и r. По теореме Пифагора найдем r:
.
Теперь находим площадь сечения:
≈706,86
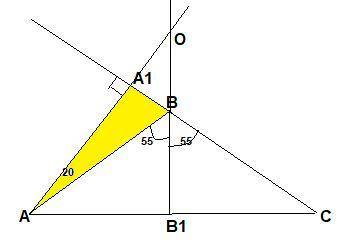
В равнобедренном треугольнике ABC угол B равен 110 градусов. Определите угол между прямой, содержащей высоту AA1, и прямой, содержащей биссектрису BB1. ответ запишите в градусах.
Объяснение:
Высота АА₁ падает на продолжение стороны ВС, т.к ∠АВС тупой. Тогда углом между между прямой, содержащей высоту AA₁, и прямой, содержащей биссектрису BB₁ будет∠АОВ₁ .
Угол АВС внешний для Δ АВА₁, значит ∠ВАА₁=110°-90°=20°.
ΔАВС-равнобедренный, углы при основании равны
∠ВАС=(180-110°):2=35° → ∠В₁АО=35°+20°=55°.
Δ АОВ₁ -прямоугольный , ∠АОВ₁=90°-55°=35°
7,68 см
Объяснение:
Прямая: M N P
MP = 12,8 см
NP = 1,5 MN
MP = MN + NP
MP = MN + 1,5 MN
MP = 2,5 MN
2,5 MN = 12,8
MN = 5,12 см
MP = 12,8 - 5,12 = 7,68