
ВМ=1
ВК=1
АМ=4
АР=4
КС=6
РС=6
Объяснение:
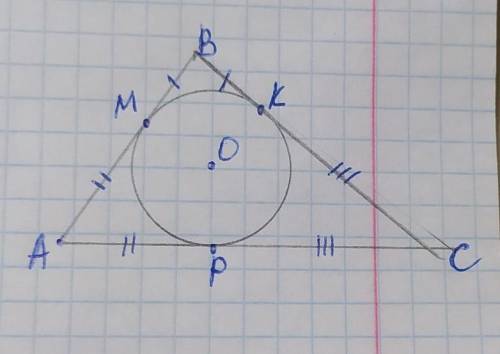
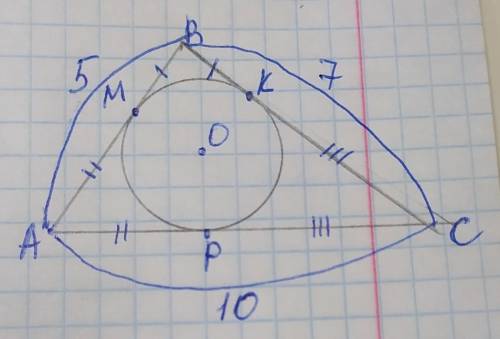
обозначим вершины треугольника А В С, точки касания М, К, Р, а центр вписанной окружности О. Стороны треугольника являются касательными к вписанной окружности, и отрезки касательных соединяясь в одной вершине равны от вершины до точки касания, поэтому: ВМ=ВК, АМ=АР, КС=РС. Пусть ВМ=ВК=х, тогда АМ=РМ=5–х, КС=РС=7–х. В этом случае сторона АС=АР+РС. Составим уравнение:
(5–х)+(7–х)=10
5–х+7–х=10
–2х+12=10
–2х=10–12
–2х= –2
х= –2÷(–2)
х=1
Итак: ВМ=ВК=1, тогда АМ=АР=5–1=4
КС=РС=7–1=6
Объяснение:
1. Найдите градусную меру угла С треугольника АВС, если А = 120, В = 40.
Решение.
180°-(120°+40°)=180°-160°=20°.
***
2. В треугольнике АВС угол С прямой, А = 30, АВ = 16 см. Найдите ВС.
ВС - катет. АВ -- гипотенуза. Угол А=30°.
Катет, лежащий против угла в 30° равен 1/2 гипотенузы. ВС= 1/2 * 16 = 8 см.
***
3. В треугольнике ABC AC = BC. Внешний угол при вершине B равен 125°. Найдите угол C.
Внешний и внутренний углы - смежные их сумма равна 180°.
Угол В= 180° - 125°= 55°;
АВ - основание равнобедренного треугольника. Значит угол А равен углу В и равен 55°.
Угол при вершине (угол С) равен 180°-2*55°=180°-110°=70°.