Площадь полученного шестиугольника будет меньше площади данного шестиугольника на шесть площадей равных равнобедренных треугольников. У этих треугольников боковые стороны равны ½ стороны данного шестиугольника, а угол между ними равен 120⁰.
SΔ= ½ ab · sin γ
S = ½ · ¼a² · (√3)/2 =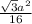 
(кв.ед.)
Из формулы площади шестиугольника S=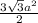
выражаем сторону а:
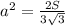
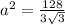
Подставляя в формулу площади треугольника, находим, что SΔ = 8/3 кв.ед.
6SΔ = 16 кв.ед.
Площадь полученного шестиугольника равна 64-16=48 (кв.ед.)
∠A = ∠C = 100°, ∠ADC = ∠B = 80°
Объяснение:
1) ∠DFB = 140° ⇒ ∠AFD = 180° - ∠DFB = 180° - 140° = 40° (∠DFB и ∠AFD смежные)
2) ABCD – параллелограмм ⇒ AB ║DC ⇒ ∠AFD = ∠FDC = 40° (накрест лежащие углы при параллельных прямых)
3) DF - биссектриса ∠ADC ⇒ ∠ADF = ∠FDC = 40° ⇒ ∠ADC = ∠ADF + ∠FDC = 40° + 40° = 80° ⇒ ∠B = 80° (∠ADC = ∠B, т.к. противолежащие углы параллелограмма равны)
4) ∠А = ∠С = 180° - 80° = 100° (∠А = ∠С, т.к. противолежащие углы параллелограмма равны)