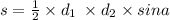
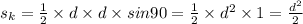
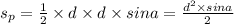
Середины сторон четырехугольника являются вершинами параллелограмма (теорема Вариньона). Стороны параллелограмма Вариньона параллельны диагоналям четырехугольника и равны их половинам (т.к. являются средними линиями в треугольниках, образованных сторонами и диагоналями).
Диагонали равнобедренной трапеции равны, следовательно стороны параллелограмма Вариньона равны и он является ромбом.
MN - средняя линия в ABC => MN||AC, MN=AC/2. Аналогично LK||AC, LK=AC/2.
MN||LK, MN=LK => MNKL - параллелограмм (противоположные стороны параллельны и равны).
AC=BD, NK=BD/2 => MN=NK => MNKL - ромб (смежные стороны равны).
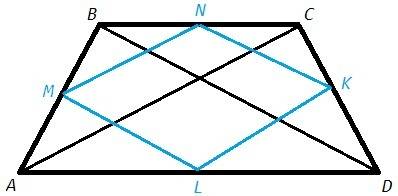
Объяснение:
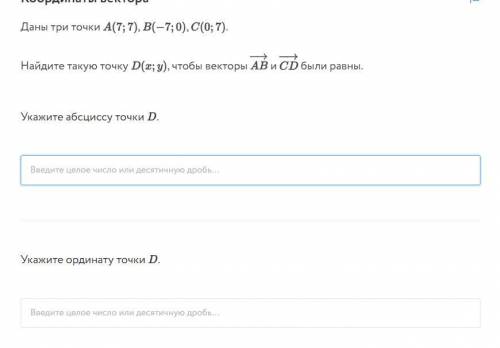
A( 7 ; 7 ) , B(- 7 ; 0 ) , C( 0 ; 7 ) ; D( x ; y ) - ?
Вектори AB i CD - рівні ; визначаємо коорд . цих векторів :
вектори АВ(- 14 ;- 7 ) і CD( x ; y - 7 ) , тоді із рівності векторів
x = - 14 - абсциса точки D ;
y - 7 = - 7 ; > y = - 7 + 7 ; >
y = 0 - ордината точки D .