Углы B и C в рассматриваемом равнобедренном треугольнике равны (как углы между основанием и равными рёбрами). Их градусную меру можно определить через известное значение косинуса
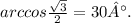
Площадь треугольника найдём как сумму двух одинаковых площадей прямоугольных треугольников. Для этого проведём из вершины A высоту на основание BC. Эта высота AF для равнобедренного треугольника будет также биссектрисой угла A и медианой, делящей основание BC пополам.
Сумма углов треугольника ABC равна 180°. Значит, угол A будет равен 180° - 30° - 30° = 120°. Половина угла равна 60°.
Итак, имеем два равных треугольника ABF и ACF с углами B=C=30° и гипотенузами AB=AC=6. Высоту AF найдём как произведение гипотенузы AB на косинус угла BAF = 0,5 углов A = 60°: AF = 6 · 0,5 = 3. Половину основания найдём из теоремы Пифагора:
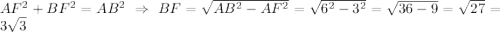
Проверим, зная косинус угла B:
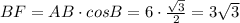
Площадь прямоугольного треугольника равна половине произведения его катетов. Полная площадь равнобедренного треугольника равна сумме площадей равных треугольников ABF и ACF. Получим:
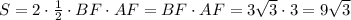
Основание равнобедренного треугольника АВС - сторона ВС, так как прямая,параллельная основанию равнобедренного треугольника АВС пересекает стороны АВ и АС в точках М и N на сторонах АВ и АС по условию. Значит <ABC=<ACB как углы при основании.
Углы <AMN=<ABC и <ANM=ACB как соответственные углы при параллельных прямых MN и BC и секущих АВ и АС соответственно. Следовательно, треугольник MАN равнобедренный с основанием MN, так как углы при стороне MN равны между собой.
Что и тоебовалось доказать.