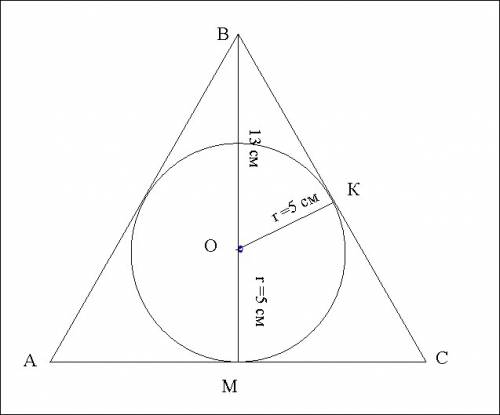
Дано: ΔАВС
АВ=ВА
(О; r) - вписанная окр.
ВМ⊥АС
ВО=13 см
ОК= r = 5 см
Найти: Р ΔАВС
1) Из прямоугольного ΔВОК по теореме Пифагора
ВК² = ВО² - ОК²
ВК² = 13²- 5² =169-25=144
ВК=√144 = 12 см
2) ∆ОВК~∆МВС (подобен), т.к. оба прямоугольные с общим углом ∠МВС.
Соответственные стороны пропорциональны:
ВМ : МС = ВК : ОК
18 : МС = 12 : 5
МС =18 · 5:12 = 7,5 см
АС = 2 · МС = 2·7,5 = 15 см.
3) По теореме Пифагора из ∆ВМС найдем ВС.
ВС² = ВМ² + МС²
ВС² = 18² + 7,5² = 324 + 56,25 = 380,25
ВС=√380,25 = 19,5 см
4) АВ = ВС = 19,5 см
АС = 15 см
Р= АВ+ВС+АС
Р = 2*19,5 + 15 = 54 см
ответ: 54 см
Поставим точки А на верхнем основании, В на нижнем. Отрезок d по условию есть расстояние, значит перпендикулярен и АВ, и оси ОО', и их проекциям.
На виде сверху (вдоль оси ОО') АО=ВО=r, половина проекции [АВ]/2 и d образуют прямоугольный тр-к, [AB]²=4(r²-d²).
На виде сбоку прямая АВ, её проекция [АВ] и высота h тоже образуют прямоугольный ∆, АВ²=[АВ]²+h², подставим сюда [АВ]² и получим уравнение связи: АВ²=4(r²-d²)+h².
а) выражаем искомое h, подставляем данные и получаем h=√(169-400+256)=5 дм
б) выражаем искомое d, подставляем, получаем d=√[(100+36-100)/4]= 3 см
ответ: h=5 дм, d=3 см