
Объяснение:
Один угол - х, другой угол у;
система уравнений:
х-у=60
х+у=180
решаем методом сложения:
2х=240
х=120°
у=180-120=60°;
стороны ромба и его меньшая диагональ образуют равнобедренный треугольник со сторонами - стороны ромба и основанием - меньшая диагональ. Углы при основании равны:
(180-60)/2=60° ⇒ треугольник равносторонний со стороной 16 см ⇒
периметр ромба = Р=16*4=64 см.
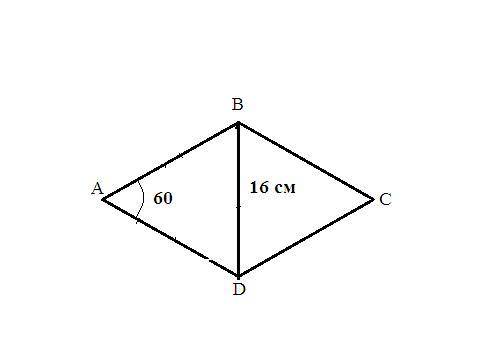
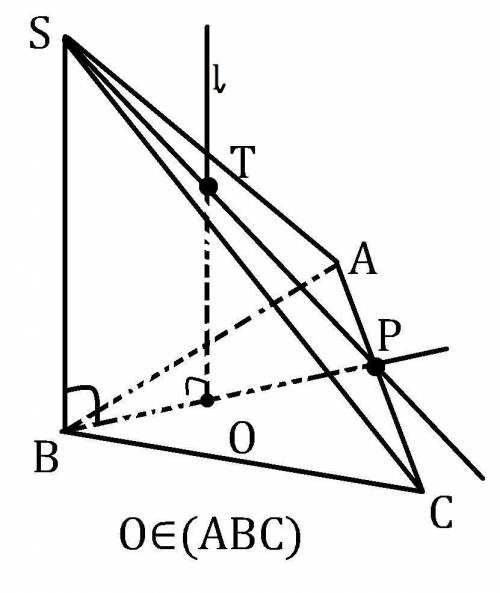
Рисунок к вопросу не был приложен, поэтому возможно пирамида выглядит по другому, но построения нужной точки остаётся правильным.
B,O∈(ABC); BO⊂(ABC); AC⊂(ABC). Пусть BO∩AC=P. *по рисунку O - лежит в треугольнике, поэтому прямые BO и AC не могут быть параллельными, а раз они лежат в одной плоскости, то они пересекаются.
O∈BP⊂(SBP) ⇒ O∈(SBP). O∈l; l║SB; SB⊂(SBP) из всего этого следует, что l⊂(SBP). SP⊂(SBP)
Ну и желательно оговорить почему прямые l и SP не параллельны. l⊥(ABC), BP⊂(ABC) ⇒ l⊥BP. Если l║SP, то SP⊥BP поскольку P∈BP. Получается, что из вершины S проведены две не совпадающие высоты к одной плоскости (ABC), что не возможно. Как итог l не параллельно SP, а раз они лежат в одной плоскости (SBP), то они пересекаются.
Пусть l∩SP=T. T - искомая точка, поскольку T∈SP⊂(SAC)
ответ: l∩(SAC)=T.
Это было доказательство того, что построение верное.
Так как Abcd- ромб, зн. Ао=ос,во=оd,Ab=bc=cd=da. Когда разность двух углов ромба равна 60°,значит угол А- угол В=60°.Возьмем через х неизвестный угол. А тогда большой угол будет 2х.Сделаем уравнения:
2х-х=60
Х=60
Тогда 2х=120°.Рассмотрим треугольник АВО.Угол ВАО=60°
Угол АВО=30°
Угол АОВ=90°
Мы знаем, что катет, который лежит напротив угла в 30° равен Одну вторую гипотенузы. Значит Ав=2АО=16см.
Равсd=16*4=64cм