TMNK- равнобедренная трапеция вписана окружность. Площадь трапеции 125. Хорда, параллельная основаниям , проведена в точки касания боковых сторон и равна 8. Найдите площадь круга.
Объяснение:
S(круга)= π R². R-?
1) Пусть О-центр вписанной окружности, ОА=ОР=ОY=R.
S (трапеции) =1/2*h*(a+b) , h=2R , (a+b)/2- длина средней линии.
2) Проведем среднюю линию НС. Она будет параллельна АВ, и пройдет через центр О (по свойству противоположных сторон описанного четырехугольника)
3) Т.к АВ параллельна основаниям , то ∠АХО=90° , тк радиус проведенный в точку касания перпендикулярен касательной.
ΔАХО-прямоугольный , cos∠ОАХ=АХ/АО , cos∠ОАХ=4/R
4) ∠ОАХ=∠АОН , тк АХ|| НО , АО-секущая.
ΔАОН-прямоугольный, cos∠ОАН=АО/НО, 4/R= R/НО ,4HO=R², 2(2HO)=R², HC=R²/2,
5) S (трапеции) =1/2 *(a+b) *h или 125= R²/2*2R , 125=R ³, R=5
S(круга)= 25π ед².

 ед².
ед².
Объяснение:Обозначим данную пирамиду буквами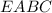 .
.
Проведём высоту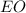 . Точка
. Точка 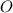 - центр
- центр 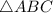 - точка пересечения, медиан, высот и биссектрис треугольника.
- точка пересечения, медиан, высот и биссектрис треугольника.
Проведём апофему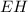 (апофема - это высота боковой грани пирамиды, проведённая из вершины пирамиды) к стороне
(апофема - это высота боковой грани пирамиды, проведённая из вершины пирамиды) к стороне 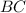 основания пирамиды.
основания пирамиды.
Т.к. данная пирамида - правильная, треугольная ⇒ основание пирамиды - правильный треугольник.
Проведём высоту в
в 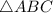 .
.
Т.к.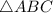 - равносторонний ⇒
- равносторонний ⇒  - высота, медиана, биссектриса.
- высота, медиана, биссектриса.
Высота и апофема
и апофема 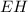 имеют общее основание, а именно точку
имеют общее основание, а именно точку 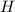 , т.к.
, т.к.  - медиана, а апофема
- медиана, а апофема 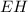 делит
делит 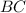 пополам (по свойству).
пополам (по свойству).
Рассмотрим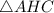 :
:
Найдём высоту по теореме Пифагора:
по теореме Пифагора: 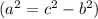
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Точка O - пересечение медиан и делит их в отношении 2 : 1, считая от вершины.
Рассмотрим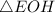 :
:
Если угол прямоугольного треугольника равен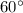 , то напротив лежащий катет равен произведению меньшего катета на
, то напротив лежащий катет равен произведению меньшего катета на 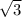 .
.
Найдём апофему по теореме Пифагора: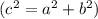
====================================================
⇒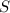 бок. поверх. =
бок. поверх. = 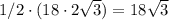 ед².
ед².
⇒ полн. поверх. =
полн. поверх. =  ед².
ед².