пусть в прямоугольном тр-ке авс угол с равен 90 градусов, угол в равен 30 градусов, гипотенуза ав=8 и из вершины прямого угла на гипот-зу проведена высота ад.1) катет, лежащий против угла 30 градусов, равен половине гипотенузы, значит ас=8/2=4. тогда по теореме пифагора вс^2=ab^2-ac^2=64-16=48.2)
по свойству высоты прямоуг-го тр-ка, проведенной к гипотенузе: катет есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу. тогда ac^2=ab*ad; => 4^2=8*ad; => ad=16/8=2 (см). значит db=ab-ad=8-2=6 (см)
не уверена решено верно или нет(катет на
против угла в 30 градусов=половине гипотенузе(по свойству)=> он равен 4см. по т. пифагора находим оставшийся катет: 8(в квадрате)=4(в квадрате)+х(в квадрате)х=4корня из дальше рассмотрим треугольник, который образовался когда провели катет напротив угла в 30 градусов = половине гипотенуза
=4корня из 3=> катет =2корня из 3. дальше по теореме пифагора находим, что один из отрезков =6 см(4корня из 3(все это в квадрате)=2корня из 3(все это в квадрате) +х(в квадрате)и остается: 8-6=2ответ: 6см, 2 см
1. Написать уравнение окружности в общем виде, изобразить на координатной плоскости.
2. Выполнив построение, выясните взаимное расположение окружности и прямой, заданных уравнениями:
у=(х+2)2+(у+1) 2=4 ,у= –х+1 .В ответе написать пересекаются, не пересекаются, касаются
3. Написать окружности прямой, с центром в точке О(1;1) и радиусом 2 см.
Объяснение:
1.Уравнение окружности (x – х₀)²+ (y – у₀)² = R² , где (х₀; у₀)-координаты центра.
2. (х+2)²+(у+1) ²=4 окружность с центром в точке (-2;-1) , радиусом 2
у= –х+1
(х+2)²+(-х+1+1) ²=4
(х+2)²+(2-х) ²=4
х²+4х+4+4-4х+х²=4
2х²=-8 или х²=-4 корней нет ⇒ не пересекаются.
3) (x – 1)²+ (y – 1)² =4
Объяснение:
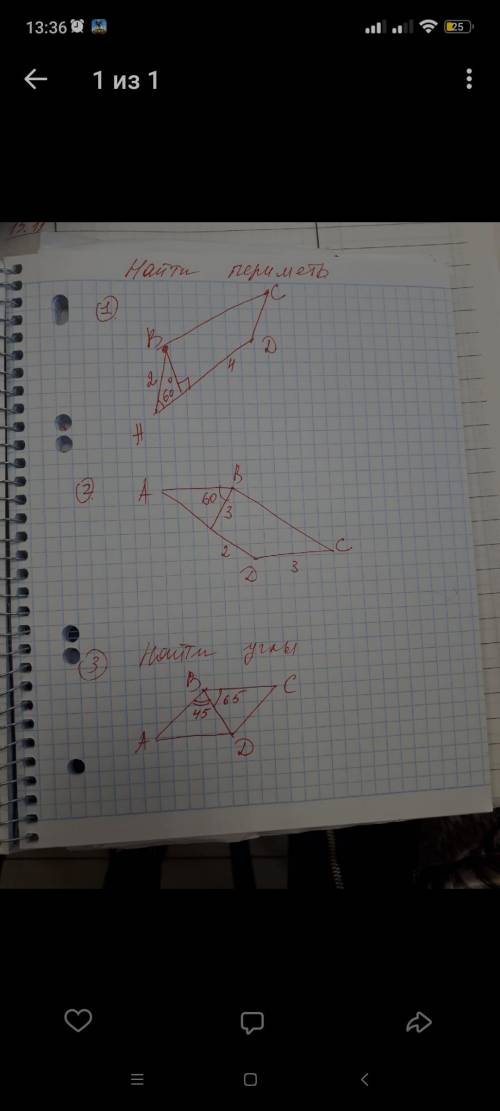
1
ВН-высота
cos60=AH/AB
AH=AB×cos60=2×1/2=1
AD=AH+HD=1+4=5
CD=AB=2
BC=AD=5
P=2(AB+AD)=2(2+5)=14
2
AB=DC=3
AB=BH=3
Тр-к АВН - равнобедренный, т. к АВ=ВН
<А=<ВНА=(180-60)/2=60
Тр-к АВН - равносторонний
АН=АВ=ВН=3
АD=AH+HD=3+2=5
BC=AD=5
P=2(DC+AD)=2(3+5)=16
3
<ABC=<ABD+<DBC=45+65=110 градусов
<A=180-<ABC=180-110=70 градусов
<C=<A=70 градусов
<АDC=<ABC=110 градусов