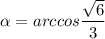
Объяснение:
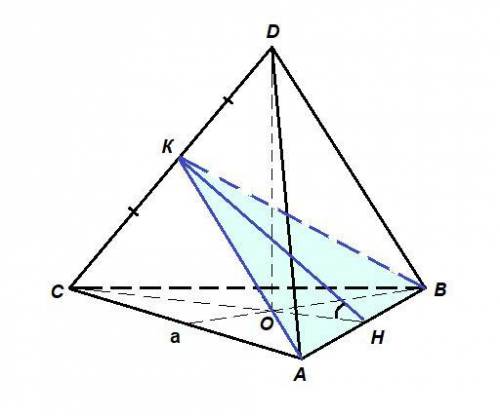
Пусть К -середина CD.
Тетраэдр правильный, все грани - правильные треугольники, тогда АК⊥CD как медиана и высота ΔACD, ВК⊥CD как медиана и высота ΔBCD, значит плоскость (АВК)⊥CD.
АК = КВ (медианы равных равносторонних треугольников)
Пусть Н - середина АВ.
СН⊥АВ как медиана и высота ΔАВС, КН⊥АВ как медиана и высота равнобедренного треугольника АКВ, значит
∠КНС - линейный угол двугранного угла между плоскостями (АКВ) и (АВС) - искомый.
∠KCH = α.
Пусть а - ребро тетраэдра.
 - высоты равных равносторонних треугольников,
- высоты равных равносторонних треугольников,
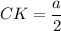
Из прямоугольного треугольника АКН по теореме Пифагора:
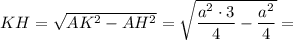
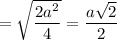
Из ΔКНС по теореме косинусов:
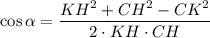
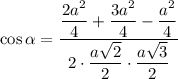

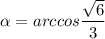
Угол между плоскостями - это линейный угол, образованный сечением этих плоскостей плоскостью, перпендикулярной к их линии пересечения.
В нашем случае это угол DHD1, где DH и HD1 - перпендикуляры к АВ. В прямоугольном треугольнике DHD1 с прямым углом D1 катет HD1 равен HD1=HD*Cosβ. Cosβ=√(1-sin²β)=√(1-1/16)=√15/4. Тогда HD1=((9*√5)/4)*(√15/4)=45√3/16. Площадь параллелограмма равна S=a*h, где а - сторона параллелограмма, а h - высота, опущенная на эту сторону. В нашем случае а=9, h=45√3/16.
S=9*45√3/16=405√3/16