Так как у нас правильная пирамида, то основание - правильный треугольник, т.е. треугольник, у которого все стороны равны, значит каждая сторона равна = 6см
Но тебе я советую прочитать заново теорию про правильные пирамиды и про правильные фигуры в стереометрии в общем, так как дальше ты уже не сможешь решать.
1. При пересечении двух прямых образуются два смежных и два вертикальных угла. Сумма смежных равна 180 радусов, значит 150 - это сумма вертикальных. Вертикальные углы равны, значит каждый угол равен 150:2=75.
3. Нам даны смежные углы, потому что один больше другого. Пусть меньший угол равен х, тогда больший угол 8х. сумма двух углов х+8х, а по теореме о смежных углах 180. Уравнение: х+8х=180 9х=180 х= 180:9 х=20, тогда 8х=8*20=160 ответ: При пересечении двух прямых образовались два угла по 20 градусов и два угла по 160 градусов каждый.
4. Угол в 120 градусов будет смежным. Поэтому угол образованный биссектрисой равен 180-120=60. Он же является половиной угла, который просят найти, значит искомый угол равен 60*2=120.
Внешний угол при вершине треугольника равен сумме внутренних углов треугольника, не смежных с ним. рассмотрим треугольник abc. угол свн - внешний угол при вершине, противоположной основанию. вм- биссектриса этого угла. она делит угол на два равных угла 1 и 2. так как внешний угол при в равен сумме внутренних углов а и с, а треугольник авс равнобедренный и углы при его основании равны между собой, все выделенные углы также равны между собой. углы под номером 1 -равные соответственные при прямых ас и вми секущей авуглы под номером 2 - равные накрестлежащие при прямых ас и вми секущей всесли при пересечении двух прямых третьей внутренние накрестлежащие углы равны, то прямые параллельны.
6 см
Объяснение:
Так как у нас правильная пирамида, то основание - правильный треугольник, т.е. треугольник, у которого все стороны равны, значит каждая сторона равна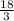 = 6см
= 6см
Но тебе я советую прочитать заново теорию про правильные пирамиды и про правильные фигуры в стереометрии в общем, так как дальше ты уже не сможешь решать.