
Уравнение окружности имеет вид 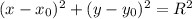 , где
, где 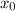 и
и 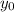 - координаты центра окружности, а
- координаты центра окружности, а 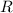 - её радиус.
- её радиус.
Координаты центра заданной окружности (2; 6).
1. То, что окружность касается оси Ох, значит, что её радиус равен расстоянию от центра окружности до оси абсцисс. На оси Ох ордината равна нулю, а значит, радиус окружности равен 6. Таким образом, уравнение окружности в этом случае:  .
.
2. То, что окружность касается оси Оy, значит, что её радиус равен расстоянию от центра окружности до оси ординат. На оси Oy абсцисса равна нулю, а значит, радиус окружности равен 2. Таким образом, уравнение окружности в этом случае: 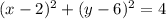 .
.
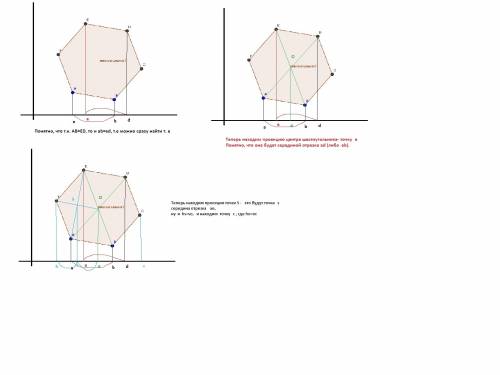
Задача 1
За узагальненою теоремою Фалеса: .
.
Знаходимо з цього рівняння x:
Відповідь: 3.
Задача 2
Нехай AK=2x, KB=3x, BM=y, MC=10-y.
За узагальненою теоремою Фалеса: .
.
Знаходимо y:
Отже, MC=10-y=10-6=4 (см).
Відповідь: 4 см.